Next: Table of Contents
![\includegraphics[width=110mm]{joonised/raamPiirk5eSnTiitel.eps}](img13.png)

|
This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/3.0/ or send a letter to Creative Commons, 543 Howard Street, 5th Floor, San Francisco, California, 94105, USA.
|
![\includegraphics[width=50pt]{joonised/cc-GPL-a.eps}](Cc-gnu_gpl.png)
|
Programs excerpts in the book are subject to the terms of the GNU GPL programs License 2.0 or later. To view a copy of the GNU General Public License license, visit
http://www.gnu.org/licenses/old-licenses/gpl-2.0.html or write to the Free Software Foundation, Inc.
51 Franklin Street, 5th Floor, Boston, MA 02110-1301, USA.
|
Mente et manu
The development of sparse matrix algorithms has led to changes in computational
structural mechanics and in the corresponding methods of analysis. The EST method
is a most general method of analysis for framed structures: beams, trusses, and frames.
In this method, compatibility equations for displacements and equilibrium equations for the member end forces at joints are incorporated.
This book considers the solving of boundary value problems of frames, beams and trusses with the
EST method. The boundary value problem (differential equations together with a set of
boundary conditions) is well posed in the method. Solutions to differential equations are represented with the initial parameter method (see also the universal equation of elastic curve of a beam [KL09] and the transfer matrix method). Kinematic
and static boundary conditions are composed by a computer program. A frame
member has 6 initial parameters and 6 end variables (3 displacements and 3 forces).
There are
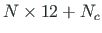 unknowns in the system of sparse equations for a frame
(
unknowns in the system of sparse equations for a frame
(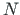 is the number of elements,
is the number of elements, 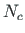 - that of
support reactions).
To assemble and solve boundary problem equations, the following steps are to be made:
- that of
support reactions).
To assemble and solve boundary problem equations, the following steps are to be made:
Round-off errors are reduced by scaling (multiplying) the displacements and rotations by the basic stiffness (scaling multiplier). After solving a system of equations for boundary value problem, the displacements and rotations found are divided by the basic stiffness.
In Chapter 1 of the book, a brief introduction to the fundamental relations of a frame element is given. Chapter 2 deals with the derivations of the EST method equations. The GNU Octave function LaheFrameDFIm.m of assembling and solving the boundary problem has been tested 0.2 with different input data (frames) shown in Chapter 3. The procedure of computing statically determinate frames with or without the displacements and rotations (with or without the compatibility equations of the displacements at joints) is considered in Chapter 4. Second-order structural analysis and the EST method for a second-order theory are treated in Chapters 5 and 6. Chapters 7 and 8 deal with the incremental loading method of plastic analysis for framed structures. A full plastic moment at a plastic hinge is described by the side conditions of the EST method.
The book deals with equations in sparse matrix form. Appendix A contains a summary of sparse matrices. Descriptions and links to the GNU Octave programs of the EST method are presented in Appendix D.
The motivation to compose the EST method has come from the books
[PL63], [Krä90], [Krä91a], [Krä91b],
[KW90], and [Krä91c]. The method outlined in
[Lah97a], [Lah97b], and [Lah98a]
differs from the transfer matrix method [PL63], [LT80]
and boundary element method [Str89], [Har87], [BW80].
I am obliged to Aime-Rutt Hall for correcting my English.
This book is dedicated to the memory of my wife Lilja.
Andres Lahe