Next: 2.2.1 Compatibility conditions at Up: 2. Equations of the Previous: 2.1 Basic equations of
Consider a system of compatibility equation sets of the joint displacements shown in excerpts 2.1 and 2.2 from the computing diary.
===============================================================
Element | Displacements | Joint | Axial, shear, moment hinges
No | u_ w_ fi_ | (node) | 0 - hinge 'false'
| indexes | No | 1 - hinge 'true'
----------------------------------------------------------------
1 1 2 3 2 0 0 0
2 19 20 21 2 0 0 0
In excerpt 2.1 from the computing diary, two elements, 1 and 2, at
joint node 2 are shown.
The displacements of element 1 at node 2 are 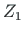 ,
, 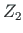 ,
, 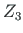 and the
displacements of element 2 at node 2 are
and the
displacements of element 2 at node 2 are 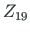 ,
, 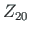 ,
, 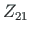 . The joint at node 2 is
rigid (see Fig. 1.12).
. The joint at node 2 is
rigid (see Fig. 1.12).
We now connect elements 1 and 2, the end displacements of which are
The compatibility equations at node 2 in global coordinates:
where the transformation matrices are expressed as
===============================================================
Element | Displacements | Joint | Axial, shear, moment hinges
No | u_ w_ fi_ | (node) | 0 - hinge 'false'
| indexes | No | 1 - hinge 'true'
----------------------------------------------------------------
2 13 14 15 4 0 0 0
3 25 26 27 4 0 0 0
4 43 44 45 4 0 0 1
In excerpt 2.2 from the computing diary, three elements - 2, 3 and
4 - at joint node 4 are shown.
The displacements of element 2 at node 4 are 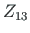 ,
, 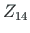 ,
, 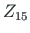 , and the
displacements of element 4 at node 4 are
, and the
displacements of element 4 at node 4 are 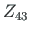 ,
, 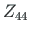 ,
, 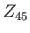 .
Element 4 has a bending moment hinge at node 4 (see Fig. 1.12).
.
Element 4 has a bending moment hinge at node 4 (see Fig. 1.12).
Now we connect elements 2 and 4, the end displacements of which are
There may be a number of displacement pairs of elements: 2-3, 2-4, 3-4, .... The set of pairs 2-3, 2-4, 3-4 is linearly independent. We need a maximal linearly independent subset of the set pairs. A linearly independent set is called maximal if each of its proper superset is linearly dependent [OUD10], [KB95]. Compatibility requirements should be satisfied in the compatibility method, called also the matrix force method. We should note that at rigid joint frames, the multiple hinge is equivalent to n-1 simple hinges (n is the number of members connected in the joint). Here, compatibility equations must be verified to meet all the criteria of transitivity 2.4. We consider pairs 2-3, 2-4 or pairs 2-3, 3-4, which are linearly independent sets.
![\begin{picture}(45,30)
\centering
\includegraphics[width=30mm]{joonised/tranitiivsus.eps}
\end{picture}](img205.png)
|
|
A relation between element end displacements is transitive whenever a displacement at bar 1 end point is equal to a displacement at bar 2 starting point, and
a displacement at bar 3 end point is equal to a displacement at bar 2 starting point.
Then the displacement at bar 1 end point is equal to the displacement at bar 3 end point (see Fig. 2.1).
|
Let us now consider the compatibility of displacements and rotations at the joints.
Displacements at joint A3 (see Fig. 2.2). Here, two elements are connected at a rigid joint.
Displacements at joint A2 (see Fig. 2.3). Here, two elements are connected at a hinged joint.
Displacements at joint B3 (see Fig. 2.4).
Three elements are connected at a rigid joint.
The displacement compatibility for elements 1-2 is given as
The displacement compatibility for elements 2-3 is given as
Displacements at joint B32 (see Fig. 2.5). Three elements are gathered together at a joint with rigid and pin connection. Elements 2-3 are connected at the joint by a hinge.
or
Elements 1-2 are connected rigidly at the joint. Their displacement compatibility equations are
or
Elements 2-3 are also connected by a hinge.
The transformation matrices
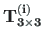 and
and
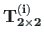 (in the program as
(in the program as
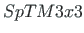 and
and 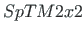 ) are represented with the functions SpTeisendusMaatriks.m
and
SpTeisendusMaatriks2x2.m, respectively.
The program selects the row index and finds column and element indexes (see excerpts 2.1 and 2.2 from the computing diary). Taking into account the expressions
) are represented with the functions SpTeisendusMaatriks.m
and
SpTeisendusMaatriks2x2.m, respectively.
The program selects the row index and finds column and element indexes (see excerpts 2.1 and 2.2 from the computing diary). Taking into account the expressions
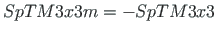 and
and
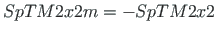 ,
the compatibility equations of the displacements at a node can be inserted into Eq. (2.1). The program inserts the transformation
matrices with the commands cmd = spA=spInsertBtoA(spA,34,43,SpTM3x3); and cmd = spA=spInsertBtoA(spA,34,25,SpTM3x3m); (see excerpt 2.3).
,
the compatibility equations of the displacements at a node can be inserted into Eq. (2.1). The program inserts the transformation
matrices with the commands cmd = spA=spInsertBtoA(spA,34,43,SpTM3x3); and cmd = spA=spInsertBtoA(spA,34,25,SpTM3x3m); (see excerpt 2.3).
#==================================================================== ----- Sparse matrix instantiation -------- spA=sparse(NNK,NNK) spA = Compressed Column Sparse (rows = 67, cols = 67, nnz = 0 [0%]) ----- Right-hand side of the equations (RHS). -------- B=zeros(NNK,1); #==================================================================== ----- Writing basic equations of a frame ---- #==================================================================== ----- Basic equations are inserted into spA -------- rows = rows_of_basic_equations: 30 col = cols_of_basic_equations: 60 spA_nnz = non_zero_elements_in_basic_equations: 95 #==================================================================== Compatibility equations of displacements at nodes From_row = Compatibility equations begin from row: 31 #==================================================================== Node = 1 Node = 2 cmd = spA=spInsertBtoA(spA,31,19,SpTM3x3); cmd = spA=spInsertBtoA(spA,31,1,SpTM3x3m); Node = 3 Node = 4 cmd = spA=spInsertBtoA(spA,34,43,SpTM3x3); cmd = spA=spInsertBtoA(spA,34,25,SpTM3x3m); cmd = spA=spInsertBtoA(spA,37,43,SpTM3x3); cmd = spA=spInsertBtoA(spA,37,13,SpTM3x3m); Node = 5 Node = 6 cmd = spA=spInsertBtoA(spA,40,55,SpTM3x3); cmd = spA=spInsertBtoA(spA,40,37,SpTM3x3m); ----- spA_rows = 42 spA_cols = 60 spA_nnz = non_zero_elements_in_spA: 129 --- Compatibility equations of displacements are inserted into spA --- compatibility_equations_rows = 12 non_zero_elements_in_compatibility_equations = 34 #====================================================================