Next: 1.3 The system equations Up: 1.2 Basic equations for Previous: 1.2.2 Basic equations for
We consider a frame element with loads applied between the ends (Fig. 1.11).
Here, we rewrite Eq. (1.40) in the form
 is the enlarged transfer matrix
is the enlarged transfer matrix  :
:
 is the vector of displacements and forces (DaFs) of the element:
is the vector of displacements and forces (DaFs) of the element:
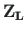 ,
,
 are the displacement and force vectors at the end and at the beginning of the element, respectively,
are the displacement and force vectors at the end and at the beginning of the element, respectively,
 is a unit matrix (for the frame element
is a unit matrix (for the frame element 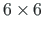 ),
),
 is the transfer matrix of Eq. (1.45) at
is the transfer matrix of Eq. (1.45) at 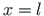 (Sign Convention 2),
(Sign Convention 2),
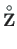 is the loading vector of Eq. (1.46) at (Sign Conventions 1 and 2).
is the loading vector of Eq. (1.46) at (Sign Conventions 1 and 2).
Note that Eq. (1.42) is a second-order equation and requires two boundary conditions, whereas Eq. (1.14) is a fourth-order equation requiring four boundary conditions. These (2+4=6) boundary conditions should be well posed. They are divided into static and kinematic boundary conditions.
The fixed-end displacements and rotation
at the end and at the beginning of the element are respectively
The fixed-end forces and the moments
 ,
,
 at the end and at the beginning of the element, respectively, are
shown in Eq. (1.52).
at the end and at the beginning of the element, respectively, are
shown in Eq. (1.52).
At unloaded joints (contacts) of elements, the sum of the fixed-end forces and moments is zero.
Sometimes the fixed-end forces and moments at joints are called internal reactions1.8 1.9 or joint contact forces1.10 [GN12]. We shall call them contact forces and contact moments.
A boundary value problem is a differential equation together with a set of boundary conditions. Solutions to the differential equations of a frame element are given with the basic system of equations (1.47). The boundary value problem should be well posed. The kinematic and static boundary conditions [KW90] of a frame element are shown in Figs. (1.10) and (1.12).