Next: 1.2.3 The basic system Up: 1.2 Basic equations for Previous: 1.2.1 The Euler-Bernoulli beam
The governing differential equation for a truss element is
 and EA denotes the axial stiffness.
and EA denotes the axial stiffness.
We now consider the basic equations of a frame element in symbolic matrix notation
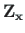 ,
,
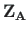 are the vectors of displacements and forces
at the point with x-coordinate and at the beginning of the element, respectively,
are the vectors of displacements and forces
at the point with x-coordinate and at the beginning of the element, respectively,
 is the transfer matrix (Sign Convention 2):
is the transfer matrix (Sign Convention 2):
 is the scaling multiplier for the displacements (
is the scaling multiplier for the displacements (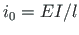 ) and the
loading vector
(yzhqz.m, yzfzv.m,
yzmyv.m) can be expressed as
) and the
loading vector
(yzhqz.m, yzfzv.m,
yzmyv.m) can be expressed as
Some other loading vectors are to be found in Tables C.1 and C.2 of Appendix C.
andres