Next: 2. Equations of the Up: 1. Introduction Previous: 1.2.3 The basic system
The total number of unknowns  in this problem is decomposed as follows:
in this problem is decomposed as follows:
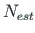 - the number of displacements and forces (see Eq. (1.50)) of the
elements,
- the number of displacements and forces (see Eq. (1.50)) of the
elements,
 (
( - the number of elements),
- the number of elements),
 ;
;
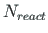 - the number of external support reactions of the frame (beam).
- the number of external support reactions of the frame (beam).
To solve this boundary value problem, it is necessary but not sufficient that the number of
linear equations 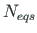 in a system of equations
in a system of equations
Both external and internal boundary conditions (Fig. 1.13) of a system (frame/beam) should be well posed.
The kinematic and static boundary conditions of the external support shown in Fig. (1.10) and these of the internal support shown in Fig. (1.12) should be well posed.
The kinematic and static boundary conditions of the internal support are divided into
It is convenien to use a sparse representation of equations (1.54) (see section A.1).
Numerical difficulties may occur when the transfer matrix manipulation involves
differences of large numbers, which can lead to inaccuracies in
computations [PW94], [PL63]. In the state vector  of equations (1.47) the displacements and rotations are small in comparison with the contact forces and moments. We will scale (multiply) the displacements and rotations by
of equations (1.47) the displacements and rotations are small in comparison with the contact forces and moments. We will scale (multiply) the displacements and rotations by
 (as a scaling multiplier for the displacements,
basic stiffness is taken).
(as a scaling multiplier for the displacements,
basic stiffness is taken).
In the sparse matrix  of Eq. (1.54), the basic equations of
the system are
described in local coordinates.
The compatible equations of displacements, joint equilibrium equations, side conditions equations and
external support reactions of the system of Eq. (1.54) are described in global coordinates.
of Eq. (1.54), the basic equations of
the system are
described in local coordinates.
The compatible equations of displacements, joint equilibrium equations, side conditions equations and
external support reactions of the system of Eq. (1.54) are described in global coordinates.
The following direction cosines allow us to transform vectors from local to global coordinates.
The direction cosines of a vector are the cosines of the angles between the vector and the coordinate axes (see Fig. 1.14):
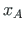 ,
,  ,
, 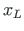 ,
, 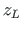 are the start point and the end point coordinates (Fig. 1.14).
are the start point and the end point coordinates (Fig. 1.14).
The two-dimensional transformation matrix
 (considered in section A.2) transforms the vector from local to global coordinates.
(considered in section A.2) transforms the vector from local to global coordinates.
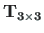 (considered in section A.2) transforms the vector from local to global coordinates.
(considered in section A.2) transforms the vector from local to global coordinates.
Note that it is possible to insert the transformation matrices of Eqs. (A.25) and (1.59) into the
sparse matrix of Eq. (1.54) with the function spA=spInsert BtoA(spA,M,N,spTi) (p. ![]() ).
).
andres