2. Equations of the EST method

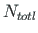
The non-symmetric sparse system of linear equations (1.54) has 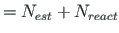$N_{totl}$ $= N_{est} + N_{react}$ unknowns (see Eq. 1.53):

$$\mathbf{spA}{\cdot}\mathbf{Z} = \mathbf{B}$$ (2.1)

The structure of the system and the sparsity pattern of the sparse matrix spA are shown in Figs. 1.13 and 3.14, respectively.

The composition of the EST method equations should be considered with GNU Octave ^{2.1 2.2} - a high-level interpreted language, primarily intended for numerical calculations [EBH08]. The GNU Octave language is quite similar to Matlab ^2.3, so that most programs are easily portable. GNU Octave is distributed under the terms of the GNU General Public License.