Next: 2.3 Equations of joint Up: 2.2 Compatibility equations of Previous: 2.2 Compatibility equations of
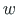 and slope
and slope 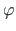 .
The two beam elements in Fig. 2.7 have a rigid connection:
.
The two beam elements in Fig. 2.7 have a rigid connection:
In Fig. 2.8, the two beam elements have a hinged connection:
andres