Next: 2.2 Compatibility equations of Up: 2. Equations of the Previous: 2. Equations of the
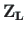 ,
,
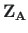 are the vectors of displacements and forces
at the end and at the beginning of the element, respectively, and
are the vectors of displacements and forces
at the end and at the beginning of the element, respectively, and
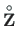 is the loading vector of the element from Eq. (1.46) at
is the loading vector of the element from Eq. (1.46) at 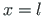 .
.
To insert the system of basic equations (2.2) into the system of Eq. (2.1), the GNU Octave functions ysplvfmhvI.m
(p. ![]() ),
yzhqz.m
(p.
),
yzhqz.m
(p. ![]() ), yzfzv.m
(p.
), yzfzv.m
(p. ![]() ),
spInsertBtoA.m
(p.
),
spInsertBtoA.m
(p. ![]() ),
InsertBtoA.m
) are used.
The procedure of inserting is given in excerpt 2.1 from the program.
),
InsertBtoA.m
) are used.
The procedure of inserting is given in excerpt 2.1 from the program.
|
|
andres