2.7 Element displacements and forces

To determine element displacements and forces, the transfer matrix is used. Calculating the internal reaction^{2.8 2.9 2.10} of Eq. (2.53) for drawing internal forces diagrams, the calculating trick is done (see Fig. 2.19).

$$\mathbf{Z_{L}\left( x\right) } = \mathbf{U}\cdot\mathbf{Z_{A}} + \mathbf{\stackrel{\rm\circ}{Z}}$$ (2.53)

where

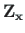$\mathbf{Z_{x}}$ is the vector of displacements and forces at x,

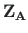$\mathbf{Z_{A}}$ - unscaled initial parameter vector (Sign Convention 2) in local coordinates (see excerpt 2.12),

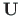$\mathbf{U}$ - transfer matrix in Eq. (1.45),

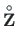$\mathbf{\stackrel{\rm\circ}{Z}}$ - load vector in Eq. (1.46),

The scaling multiplier for element displacements $\mathbf{i_{0}=1.0}$ ($i_{0}= EI/l$).

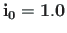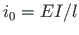Calculations of the internal reactions (internal forces correspond to Sign Convention 1) are presented in excerpt 2.13.

Figure 2.19: Cross-sectional directions

In Fig. 2.19, minus and plus cross-sectional directions are shown. The sign of the internal forces corresponds to Sign Convention 1 of the internal reactions. To calculate an internal reaction for drawing internal forces diagrams, a calculating trick is done. As the sign of the initial parameters corresponds to Sign Convention 2, the internal reactions are calculated at cross-section (Eq. (2.53)).         
        

Computing diary excerpt 2.13 ( spESTframe93LaheWFI.m )  

#------------- Element displacements and forces ---------- 
for i=1:NEARV
   krda=i;
   vF=zeros(6,12);
      EI=selem(i,13);   % from topology
      EA=selem(i,14);   %   "      "
      GAr=selem(i,15);  %   "      "
   Li=lvarras(i,1);
   qx=qxZ(i,1);
   qz=qzZ(i,1);
   aLx=aLXx(i,1);
   Fz=FZz(i,1);
   Fx=FZx(i,1);
   xsamm=Li/Nmitmeks; % element is divided into 4 parts
   xx=0;
   AP=AlgPar(i,:)';
#--------- Transfer matrix equation --------
     for ij=1:Nmitmeks+1  # 5 - displacements and forces at x=0.0
       vvF=ylfhlin(1.0,xx,EA,GAr,EI);
       vvB=yzhqz(1.0,xx,qx,qz,EA,EI);
       vvFz=yzfzv(1.0,xx,aLx,Fx,Fz,EA,EI);
       Fvv(:,ij)=vvF*AP+vvB+vvFz;
       xx=xx+xsamm;
     endfor
 ...
endfor
#-------------------------------------------------------------