8.1.2 The n=2 times statically indeterminate frame

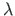Example 8.3 Problem Statement. Consider the frame depicted in Fig. 8.1 and described in Example 8.1. We wish to compute the load factor $\lambda$ (see Fig. 8.9(b)) at which the second plastic moment occurs.

**Figure 8.9:** Load cases of the n = 2 times indeterminate frame ESTsn2
$\includegraphics[width=65mm]{joonised/raamPiirk4eSn.eps}$ [ $F_{1} = 1{\,}\mathrm{kN}, F_{2} = 0.5{\,}\mathrm{kN}$ ]		$\includegraphics[width=74mm]{joonised/raamPiirk5eSn.eps}$ [ $F_{1} = 17.884{\,}\mathrm{kN}, F_{2} = 8.9422{\,}\mathrm{kN}$ ]

Problem Solving. The two load cases shown in Fig. 8.9 are applied:

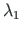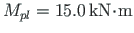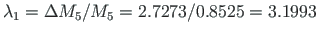Load case 1 (Fig. 8.9(a)). The load factor $\lambda_{1}$ for a moment $M_{pl} = 15.0 {\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}$ to appear at node 5 must be found. We find that for a plastic moment to appear at node 5, the load factor is to be $\lambda_{1}=\Delta M_{5}/M_{5}= 2.7273/0.8525=3.1993$ as shown in Fig. 8.3(a) ( 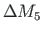$\Delta M_{5}$ was found on page ).
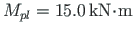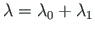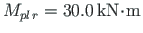Load case 2 (Fig. 8.9(b)). The boundary moments that are equal to the full plastic moment $M_{pl} = 15.0 {\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}$ are added to the ends of elements 3 and 4 at plastic hinge 4 (see excerpt 8.6). The corresponding load factor $\lambda =\lambda_{0} +\lambda_{1}$ is shown in Fig. 8.3(b). We find now that at node 3, a third full plastic moment $M_{pl\,r} = 30.0 {\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}$ appears (see Fig. 8.3(b)). 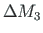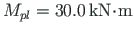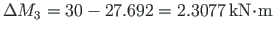We also find that $\Delta M_{3}$ is needed to add at this node to achieve $M_{pl} = 30.0{\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}$ , and that $\Delta M_{3} = 30 - 27.692 = 2.3077{\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}$ as shown in Figs. 8.3(b) and 8.4(a).

We use the EST method described in Chapter 3, ``Statically indeterminate problems'', and carry out the following steps of calculations:

Data input: the number of frame nodes, elements, support reactions; element properties, element loads in local coordinates, node forces in global coordinates, nodal coordinates, topology and hinges, side conditions, restrictions on support displacements.

$\displaystyle \mathbf{spA}{\cdot}\mathbf{Z} = \mathbf{B} \vspace*{-6pt}$ (8.2)
Assembling and solving the boundary problem equation (8.2) (prepared and solved by the function LaheFrameSnDFIm.m):
1. writing the basic equations of a frame in transfer matrix form,
2. adding the compatibility equations of the displacements at nodes,
3. adding the joint equilibrium equations,
4. adding the side conditions (moment hinges),
5. adding the restrictions on support displacements,
6. solving the system of sparse equations,
7. producing an output: initial parameter vectors for element displacements and forces; support reactions.
Output: element displacements and forces determined by the transfer matrix.

1. Input data for the GNU Octave program spESTframeSn2LaheWFI.m are given in excerpts from the program: element and nodal loads - excerpt 8.4; nodal coordinates - excerpt 8.5; element properties, topology and hinges - excerpt 8.6.

Program excerpt 8.4 ( spESTframeSn2LaheWFI.m )

 Number_of_frame_nodes=5
 Number_of_elements=4
 Number_of_support_reactions=6
 spNNK=12*Number_of_elements+Number_of_support_reactions;
 Number_of_unknowns=spNNK 
 Displacements and forces are calculated on parts ''Nmitmeks'' of the element 
 Nmitmeks=4
 Lp=10.0; % graphic axis
# ---- Load variants ----- 
load_variant=1;
#load_variant=2;
# --- Element properties ---

  
 EIp=20000 # kN/m^2
 EIr=40000 # kN/m^2
 EAp=4.6*10^6 
#EAp=4.6*10^15; 
 EAr=6.8*10^6
#EAr=6.8*10^15; 
 GAp=0.4*EAp 
 GAr=0.4*EAr

baasi0=EIp/4 # scaling multiplier for displacements # baasi0=1.0; h=4.0; l=4.0; l1=l % l l2=l % l Mplr=30.0 # The plastic moment of beam Mplp=15.0 # The plastic moment of column # Loads F2s=0.5; F3s=1.0; switch (koormusvariant) case{1} disp('--- ') disp(' Load variant 1 ') disp('--- ') # disp(' myfile31.mat Flambda0 deltaM0 muutujaDaF1 ') disp('load myfile31.mat ') load myfile31.mat # Flambda0 deltaM0 muutujaDaF1 # # Element load in local coordinates # qz qx qA qL # Uniformly distributed load in local coordinate z and x directions Loadsq on element=4; esQkoormus=zeros(LoadsqONelement,4,ElementideArv);

esQkoormus(1,1:4,1)=[0.0 0.0 0.0 4.0];
esQkoormus(1,1:4,2)=[0.0 0.0 0.0 4.0];
esQkoormus(1,1:4,3)=[0.0 0.0 0.0 4.0];
esQkoormus(1,1:4,4)=[0.0 0.0 0.0 4.0];

# # Point load in local coordinate z and x directions kN # Fz, Fx, aF (coordinate of the point of force application) LoadsF on Element=5; esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);

esFjoud(1,1:3,1)=[0.0 0.0 4.0];
esFjoud(1,1:3,2)=[0.0 0.0 4.0]; 
#esFjoud(2,1:3,2)=[0.0 0.0 4.0];
esFjoud(1,1:3,3)=[0.0 0.0 4.0]; 
esFjoud(1,1:3,4)=[0.0 0.0 4.0];

# # Node forces in global coordinates # sSolmF(forces,1,nodes); forces=[Fx; Fz; My] sSolmF = zeros(3,1,SolmedeArv);

#sSolmF(:,1,1)= 0.0;
sSolmF(1,1,2)= F2s; # 0.5;
sSolmF(2,1,3)= F3s; # 1.0;
#sSolmF(:,1,4)= 0.0
#sSolmF(:,1,5)= 0.0

# #s1F(1,1,1)=0.0; # force Fz #s1F(2,1,1)=0.0; # force Fz #s1F(3,1,1)=0.0; # force My # Support shift - tSiire# # Support shift is multiplied by scaling multiplier tSiire = zeros(3,1,SolmedeArv);

#tSiire(:,1,1)= 0.0
#tSiire(2,1,1)= 0.01*baasi0
#tSiire(:,1,2)= 0.0
#tSiire(:,1,3)= 0.0
#tSiire(:,1,4)= 0.0
#tSiire(:,1,5)= 0.0

case{2} disp('--- ') disp(' Load variant 2 ') disp('--- ') load myfile31.mat Flambda0 disp(' load myfile20.mat ') load myfile20.mat disp(' plastF1F2; ') #plastF1F2=[Flambda Flambda0 Flambda1 F2s02 F3s02] plastF1F2; Flambda=plastF1F2(1,1) Flambda0=plastF1F2(1,2) Flambda1=plastF1F2(1,3) F2s02=plastF1F2(1,4) F3s02=plastF1F2(1,5)
# Element load in local coordinates # qz qx qA qL # Uniformly distributed load in local coordinate z and x directions Loadsq on element=4; esQkoormus=zeros(LoadsqONelement,4,ElementideArv);

esQkoormus(1,1:4,1)=[0.0 0.0 0.0 4.0];
esQkoormus(1,1:4,2)=[0.0 0.0 0.0 4.0];
esQkoormus(1,1:4,3)=[0.0 0.0 0.0 4.0];
esQkoormus(1,1:4,4)=[0.0 0.0 0.0 4.0];

# # Point load in local coordinate z and x directions kN # Fz, Fx, aF (coordinate of the point of force application) LoadsF on Element=5; esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);

esFjoud(1,1:3,1)=[0.0 0.0 4.0];
esFjoud(1,1:3,2)=[0.0 0.0 4.0]; 
#esFjoud(2,1:3,2)=[0.0 0.0 4.0];
esFjoud(1,1:3,3)=[0.0 0.0 4.0]; 
esFjoud(1,1:3,4)=[0.0 0.0 4.0];

# # Node forces in global coordinates # sSolmF(forces,1,nodes); forces=[Fx; Fz; My] sSolmF = zeros(3,1,SolmedeArv);

#sSolmF(:,1,1)= 0.0;
sSolmF(1,1,2)= F2s02;
sSolmF(2,1,3)= F3s02;
#sSolmF(:,1,4)= 0.0
#sSolmF(:,1,5)= 0.0

# #s1F(1,1,1)=0.0; # force Fz #s1F(2,1,1)=0.0; # force Fz #s1F(3,1,1)=0.0; # force My # Support shift - tSiire# # Support shift is multiplied by scaling multiplier tSiire = zeros(3,1,SolmedeArv);

#tSiire(:,1,1)= 0.0
#tSiire(2,1,1)= 0.01*baasi0
#tSiire(:,1,2)= 0.0
#tSiire(:,1,3)= 0.0
#tSiire(:,1,4)= 0.0
#tSiire(:,1,5)= 0.0

otherwise disp(' No load variant cases ') endswitch

Program excerpt 8.5 ( spESTframeSn2LaheWFI.m )
#========== # Nodal coordinates #========== krdn=[# x z 0.0 0.0; % node 1 0.0 -4.0; % node 2 4.0 -4.0; % node 3 8.0 -4.0; % node 4 8.0 0.0]; % node 5 #========== # #========== # Restrictions on support displacements (on - 1, off - 0) # Support No u w fi #========== tsolm=[1 1 1 1; % node 1 5 1 1 1]; % node 5 #==========

Program excerpt 8.6 ( spESTframeSn2LaheWFI.m )
# ------------- Element properties, topology and hinges --------- elasts=[# Element properties # n2 - end of the element # n1 - beginning of the element # N, Q, M - hinges at the end of the element # N, Q, M - hinges at the beginning of the element # Mpl - plastic moment at the end of the element # Mpl - plastic moment at the beginning # of the element EIp EAp GAp 2 1 0 0 0 0 0 0 0.0 0.0 ; % element 1 EIr EAr GAr 3 2 0 0 0 0 0 0 0.0 0.0 ; % element 2 EIr EAr GAr 4 3 0 0 1 0 0 0 -Mplp 0.0 ; % element 3 EIp EAp GAp 5 4 0 0 0 0 0 1 0.0 Mplp ]; % element 4 # 1 - hinge 'true' (axial, shear, moment hinges) #

2. Assembling and solving the boundary problem equations (8.2), carried out by the function LaheFrameSnDFIm(baasi0,Ntoerkts,esQkoormus,esFjoud,sSolmF,tsolm,tSiire, krdn,selem). This function gives the unscaled initial parameter vectors of the elements and support reactions according to the load cases.

3. Output data.
Load case 1. The load factor 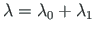$\lambda = \lambda_{0}+\lambda_{1}$ (Flambda), and forces 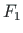$F_{1}$ (F3s02) and 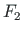$F_{2}$ (F2s02) are presented in excerpt 8.5 from the computing diary.

Computing diary excerpt 8.5 ( spESTframeSn2LaheWFI.m )
deltaM0=15.0-AbsmaxminM deltaM0 = 2.7273 -------------- absX = 0.85246 Flambda1=deltaM0/absX Flambda1 = 3.1993 Flambda=Flambda0+Flambda1 Flambda = 17.885 -------------- F2s02=Flambda*F2s F2s02 = 8.9423 F3s02=Flambda*F3s F3s02 = 17.885 ============== plastF1F2=[Flambda Flambda0 Flambda1 F2s02 F3s02] plastF1F2 = 17.8846 14.6853 3.1993 8.9423 17.8846 save myfile20.mat plastF1F2

The bending moments of the first loading case are presented in excerpt 8.2 from the computing diary, and the bending moments diagram is shown in Fig. 8.3(a).

Computing diary excerpt 8.6 ( spESTframeSn2LaheWFI.m )

Moments at nodes (Sign Convention 2) ============================================================== Node Moment DaF No Fi/baasi0 DaF No Work_b Element -------------------------------------------------------------- 1 0.95082 12 0.00000e+00 9 0.00000e+00 1 2 0.19672 6 -7.54098e-05 3 -1.48347e-05 1 2 -0.19672 24 -7.54098e-05 21 1.48347e-05 2 3 2.09836 18 1.09290e-06 15 2.29329e-06 2 3 -2.09836 36 1.09290e-06 33 -2.29329e-06 3 4 0.00000 30 7.10383e-05 27 0.00000e+00 3 4 0.00000 48 -8.52459e-05 45 -0.00000e+00 4 5 0.85246 42 0.00000e+00 39 0.00000e+00 4 --------------------------------------------------------------

Load case 2. The bending moments of the second loading case are given in excerpt 8.8 from the computing diary, and the bending moments diagram is shown in Fig. 8.3(b). We find that the next node at which a full plastic moment $M_{pl} = 30.0{\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}$ will appear is node 3 (DaF = 36, see computing diary excerpt 8.7, Figs. 8.8 and 8.3(b)). At this node, 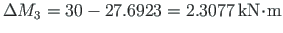$\Delta M_{3} = 30 - 27.6923 = 2.3077{\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}$ (deltaM0) is to be added as shown in excerpt 8.7 and Fig. 8.4(a).

Computing diary excerpt 8.7 ( spESTframeSn2LaheWFI.m )

The maximum absolute values of reduced moments AbsmaxminM = 27.6923 Flambda = 17.885 Flambda0 = 14.685 Flambda1 = 3.1993 deltaM0 = 2.3077 muutujaDaF2 = 36 save myfile21.mat Flambda Flambda0 Flambda1 deltaM0 muutujaDaF2

Computing diary excerpt 8.8 ( spESTframeSn2LaheWFI.m )

Moments at nodes (Sign Convention 2) ============================================================== Node Moment DaF No Fi/baasi0 DaF No Work_b Element -------------------------------------------------------------- 1 6.92308 12 0.00000e+00 9 0.00000e+00 1 2 -1.15385 6 -8.07692e-04 3 9.31953e-04 1 2 1.15385 24 -8.07692e-04 21 -9.31953e-04 2 3 27.69231 18 7.69231e-05 15 2.13018e-03 2 3 -27.69231 36 7.69231e-05 33 -2.13018e-03 3 4 -15.00000 30 5.00000e-04 27 -7.50000e-03 3 4 15.00000 48 5.67933e-19 45 8.51899e-18 4 5 15.00000 42 0.00000e+00 39 0.00000e+00 4 -------------------------------------------------------------- At node 4, the dissipation D = -(-7.50000e-03 + 8.51899e-18) = 0.00750 > 0
The dissipation D at plastic hinge 4 satisfies the condition (7.19):
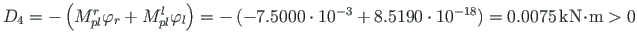${D_{4}}=-\left( M^{r}_{pl}\varphi_{r}+M^{l}_{pl}\varphi_{l}\right) = -\left(-7.... ...\right) = 0.0075{\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m} > 0$ .