Next: 8.1.1 The n=3 times Up: 8. The EST method. Previous: 8. The EST method.

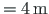 and of span
length
and of span
length
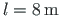 . The beam 2-4 is loaded with a vertical concentrated load
. The beam 2-4 is loaded with a vertical concentrated load 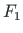
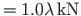 (here,
(here, 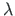 is the load factor, see Eq. (7.1)).
A horizontal load
is the load factor, see Eq. (7.1)).
A horizontal load 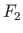
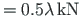 acts at joint 2. For the beam, the full plastic moment
acts at joint 2. For the beam, the full plastic moment 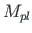
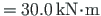 , and for the columns,
, and for the columns, 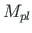
 .
.
Let us assume that the flexural rigidity of a column
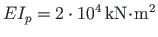 and that of the beam
and that of the beam
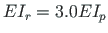 ; the axial rigidity of a column
; the axial rigidity of a column
 and that of the beam
and that of the beam
 ; the shear rigidity of a column
; the shear rigidity of a column
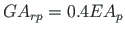 and that of the beam
and that of the beam
 .
.
We wish to compute the collapse load factor 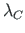 at which the frame will actually fail.
at which the frame will actually fail.
Problem Solving. We use the EST method to solve the problem of an n times statically indeterminate frame. The steps of the load incremental method are listed below.
 times
(
times
(
 , see Fig. 8.1)
to the appearance of the full plastic moment
, see Fig. 8.1)
to the appearance of the full plastic moment  . For that
. For that
 ;
;
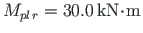 or
or
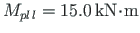 will appear.
We find that this is node 4, where
will appear.
We find that this is node 4, where
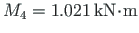 (see Fig. 8.2(a));
(see Fig. 8.2(a));
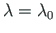 for a
moment
for a
moment
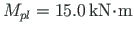 to appear at node 4.
We find that for a full plastic moment to develop at node 4, the load factor is to be
to appear at node 4.
We find that for a full plastic moment to develop at node 4, the load factor is to be
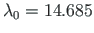 as shown in Fig. 8.2(b);
as shown in Fig. 8.2(b);
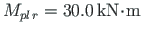 or
or 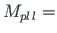
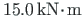 will appear.
We find that this is node 5 (see Fig. 8.2(b)).
We also find that at this node to achieve
will appear.
We find that this is node 5 (see Fig. 8.2(b)).
We also find that at this node to achieve
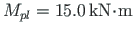 ,
, 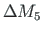 is needed to add, and that
is needed to add, and that
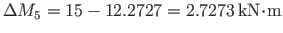 as can be seen in Figs. 8.2(b) and 8.3(a).
as can be seen in Figs. 8.2(b) and 8.3(a).
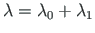 )
times to the appearance of the second full plastic moment
)
times to the appearance of the second full plastic moment 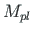 . For that
. For that
 ;
;
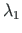 for a
moment
for a
moment
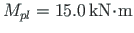 to appear at node 5.
We find that for the appearance of a plastic moment at node 5, the load factor is to be
to appear at node 5.
We find that for the appearance of a plastic moment at node 5, the load factor is to be
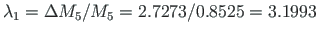 as shown in Fig. 8.3(a);
as shown in Fig. 8.3(a);
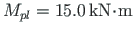 (related to
(related to  )
to the ends of elements 3 and 4 at
hinge 4 (see Fig. 8.3(b));
)
to the ends of elements 3 and 4 at
hinge 4 (see Fig. 8.3(b));
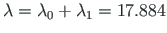 ,
the corresponding loads
,
the corresponding loads
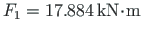 and
and
 ;
;
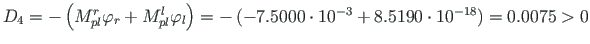 ;
;
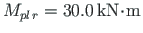 or
or  will form.
We find that this is node 3 (see Fig. 8.3(b)).
We also find that at this node,
will form.
We find that this is node 3 (see Fig. 8.3(b)).
We also find that at this node, 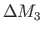 is needed to add to achieve
is needed to add to achieve
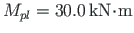 ,
and that
,
and that
 as shown in
Figs. 8.3(b) and 8.4(a).
as shown in
Figs. 8.3(b) and 8.4(a).
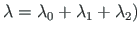 times to the appearance of the third full plastic moment
times to the appearance of the third full plastic moment 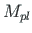 . For that
. For that
 ;
;
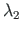 for a
moment
for a
moment
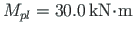 to appear at node 3.
We find that for the appearance of a plastic moment at node 3, the load factor is to be
to appear at node 3.
We find that for the appearance of a plastic moment at node 3, the load factor is to be
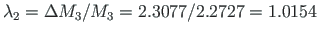 as shown in Fig. 8.4(a);
as shown in Fig. 8.4(a);
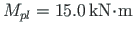 (related to
(related to 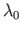 )
to the ends of elements 3 and 4 at
hinge 4 (see Fig. 8.3(b));
)
to the ends of elements 3 and 4 at
hinge 4 (see Fig. 8.3(b));
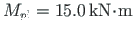 (related to
(related to 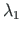 )
to the end of element 4 at plastic hinge 5 (see Fig. 8.4(b));
)
to the end of element 4 at plastic hinge 5 (see Fig. 8.4(b));
 ,
the corresponding loads are
,
the corresponding loads are
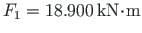 and
and
 ;
;
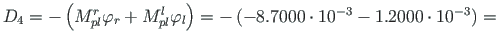
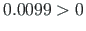 and
and
 ;
;
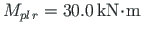 or
or 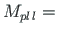
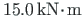 will appear.
We find that this is node 1 (see Fig. 8.4(b)).
We also find that at this node,
will appear.
We find that this is node 1 (see Fig. 8.4(b)).
We also find that at this node, 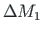 is needed to add to achieve
is needed to add to achieve
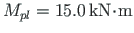 ,
and that
,
and that
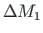
 as shown in
Figs. 8.4(b) and 8.5(a).
as shown in
Figs. 8.4(b) and 8.5(a).
 . A plastic hinge forms and the frame
becomes a mechanism. The load computed in which the moment exceeds
. A plastic hinge forms and the frame
becomes a mechanism. The load computed in which the moment exceeds
 is equal to the true collapse load.
In the n=0 times statically indeterminate (statically determinate) frame, load is increased
is equal to the true collapse load.
In the n=0 times statically indeterminate (statically determinate) frame, load is increased 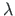 (
(
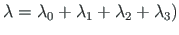 times to the appearance of the fourth full plastic moment
times to the appearance of the fourth full plastic moment  . For that
. For that
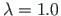 (see Fig. 8.5(a));
(see Fig. 8.5(a));
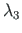 for a
moment
for a
moment
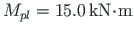 to develop at node 1.
We find that for the appearance of the plastic moment at node 1, the load factor is to be
to develop at node 1.
We find that for the appearance of the plastic moment at node 1, the load factor is to be
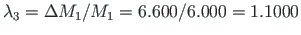 as shown in Fig. 8.5(a);
as shown in Fig. 8.5(a);
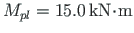 (related to
(related to 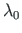 )
to the ends of elements 3 and 4 at
hinge 4 (see Fig. 8.5(b));
)
to the ends of elements 3 and 4 at
hinge 4 (see Fig. 8.5(b));
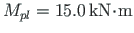 (related to
(related to 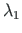 )
to the end of element 4 at plastic hinge 5 (see Fig. 8.5(b));
)
to the end of element 4 at plastic hinge 5 (see Fig. 8.5(b));
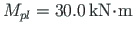 (related to
(related to 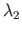 )
to the end of elements 2 and 3 at plastic hinge 3 (see Fig. 8.5(b));
)
to the end of elements 2 and 3 at plastic hinge 3 (see Fig. 8.5(b));
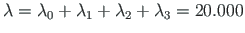 ,
the corresponding loads are
,
the corresponding loads are
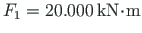 and
and
 ;
;
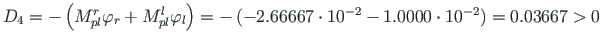 ,
,
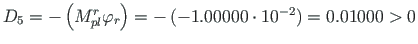 and
and
 .
.
The four
plastic hinges (nodes 1, 3, 4, and 5) produce a mechanism
leading to collapse at the loads
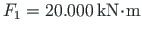 and
and
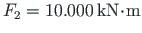 (related to the load factor
(related to the load factor
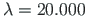 ).
).
An idealized relation between the load 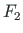 and deflection at node 3 is displayed in Fig. 8.6. The first yield moment occurs at node 4 shown in Fig. 8.5(b) and is marked with the letter A in Fig. 8.6.
The following yield moments occurring at nodes 5, 3, and 1 shown in Fig. 8.5(b) are marked with the letters B, C, D in Fig. 8.6.
and deflection at node 3 is displayed in Fig. 8.6. The first yield moment occurs at node 4 shown in Fig. 8.5(b) and is marked with the letter A in Fig. 8.6.
The following yield moments occurring at nodes 5, 3, and 1 shown in Fig. 8.5(b) are marked with the letters B, C, D in Fig. 8.6.