Next: 7.2 Methods of plastic Up: 7.1 Introduction Previous: 7.1.1 The plastic moment
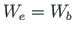 is the work done by external forces (see Appendix B.1).
is the work done by external forces (see Appendix B.1).
The work done by external forces at Sign Convention 1 (see Fig. 7.5(a))
The work done by external forces at Sign Convention 2 (see Fig. 7.5(b))
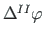 of the plastic hinge is given by the difference
between rotations of the member ends at joint.
It is necessary to check the compatibility of the rotations related to the hinge
with the sign of the plastic moment of Eq. (7.13).
of the plastic hinge is given by the difference
between rotations of the member ends at joint.
It is necessary to check the compatibility of the rotations related to the hinge
with the sign of the plastic moment of Eq. (7.13).
Considering that
 and
and
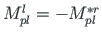 , the work of boundary forces at the member ends at joint is
, the work of boundary forces at the member ends at joint is
The boundary forces work 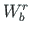 at the member end
and the boundary forces work
at the member end
and the boundary forces work
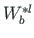 at the plastic hinge boundary, at a similar angle of rotation,
at the plastic hinge boundary, at a similar angle of rotation, 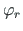 , have different signs (see Fig. 7.5(b)):
, have different signs (see Fig. 7.5(b)):
andres