Next: C. Transfer matrices Up: B. Work and work-energy Previous: B. Work and work-energy
The work-energy theorem in structural analysis: the sum of the work done by internal and external forces is zero:
 is the work done by internal forces and
is the work done by internal forces and 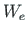 is the work done by external forces.
is the work done by external forces.
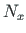 ,
, 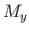 - are the internal axial force and bending moment of the first load state;
- are the internal axial force and bending moment of the first load state;
 ,
,
 - axial and bending deformations of the second load state;
- axial and bending deformations of the second load state;
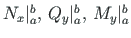 - axial force, shear force and bending moment of the first load state at boundaries a and b;
- axial force, shear force and bending moment of the first load state at boundaries a and b;
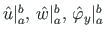 - longitudinal and transverse displacements, and the rotation of the cross section of the second
load state at boundaries a and b;
- longitudinal and transverse displacements, and the rotation of the cross section of the second
load state at boundaries a and b;
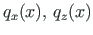 - distributed loads of the first load state;
- distributed loads of the first load state;
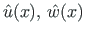 - longitudinal and transverse displacements of the second load state;
- longitudinal and transverse displacements of the second load state;
 - force components of the first load state, applied at point i in the x and z directions, respectively;
- force components of the first load state, applied at point i in the x and z directions, respectively;
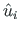 ,
,  - longitudinal and transverse displacements of point i of the second load state.
- longitudinal and transverse displacements of point i of the second load state.
The first and second elements of Eq. (B.2) describe the work  of internal forces:
of internal forces:
The final four elements of Eq. (B.2) describe the work 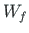 done by active forces:
done by active forces:
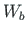 done by boundary forces
(fixed-end forces and moments at jointsB.1, support reactions):
done by boundary forces
(fixed-end forces and moments at jointsB.1, support reactions):
The external work 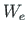 can be divided into two parts:
can be divided into two parts:
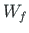 - work done by active forces, e.g. concentrated loads, uniformly distributed loads;
- work done by active forces, e.g. concentrated loads, uniformly distributed loads;
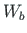 - work done by reaction forces, e.g. support reactions (Fig. 1.10), internal reactions [WP960]
(contact forces B.2)
(Fig. 1.12).
- work done by reaction forces, e.g. support reactions (Fig. 1.10), internal reactions [WP960]
(contact forces B.2)
(Fig. 1.12).
With the elastic energy
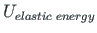 and dissipation energy
and dissipation energy 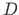 existing,
the work
existing,
the work 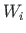 done by internal forces is in relation to the internal energy
done by internal forces is in relation to the internal energy
 :
:
Equations (B.2) and (B.7) are the basic methodical tools of structural analysis.
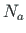 and
and 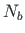 exerted on the member at cross-sections a and b
are treated as external loads [VrCty] or,
to be more precise, as boundary forces.
exerted on the member at cross-sections a and b
are treated as external loads [VrCty] or,
to be more precise, as boundary forces.
No loads act on the bar member a-b, and so 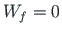 and
and 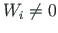 in Eq. (B.7).
The expression for energy conservation of the bar member a-b is
in Eq. (B.7).
The expression for energy conservation of the bar member a-b is