7.1.1 The plastic moment
For pure bending  , we use Eq. (7.2).
The plastic moment
, we use Eq. (7.2).
The plastic moment 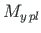 about the neutral axis y in a plastic hinge
can be computed from Eq. (7.3).
about the neutral axis y in a plastic hinge
can be computed from Eq. (7.3).
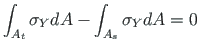 |
|
|
(7.2) |
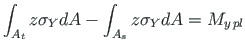 |
|
|
(7.3) |
where
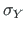 is the yield stress,
is the yield stress,
 - an area in tension,
- an area in tension,
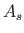 - an area in compression.
- an area in compression.
Equations (7.2) and (7.3) give
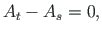 |
|
|
(7.4) |
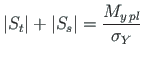 |
|
|
(7.5) |
where 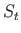 and
and 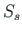 are accordingly the first moment of the area in tension and that of the area in compression about neutral axis.
are accordingly the first moment of the area in tension and that of the area in compression about neutral axis.
Figure 7.2:
Rectangular cross section
|
![\includegraphics[width=100mm]{./joonised/PiirWmom1e.eps}](img783.png)
|
From Eq. (7.5) we get the expression for the plastic moment
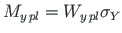 |
|
|
(7.6) |
where
the plastic section modulus is given by
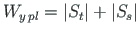 |
|
|
(7.7) |
For a rectangular cross section shown in Fig. 7.2, the plastic section modulus is
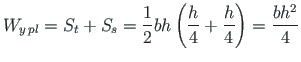 |
|
|
(7.8) |
For a rectangular cross section, the elastic section modulus is
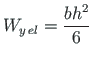 |
|
|
(7.9) |
The ratio
of the elastic section modulus to the plastic section modulus is
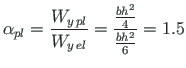 |
|
|
(7.10)
|
This ratio is termed the shape factor. The shape factor is a measure
of the efficiency of a cross section in bending. Shape factors for some cross sections are given in
Fig. 7.3.
Figure 7.3:
Shape factor 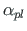 for different sections
for different sections
|
![\includegraphics[width=100mm]{./joonised/PiirWmom2.eps}](img789.png)
|
Fig. 7.4 shows stresses at loading and unloading with a pure bending moment.
At unloading, the stresses decrease (Fig. 7.4 g).
The residual stresses on the cross section after removing a moment 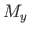 are shown in Fig. 7.4 h.
are shown in Fig. 7.4 h.
Figure 7.4:
Cross section and stresses
|
![\includegraphics[width=150mm]{./joonised/PiirMom1.eps}](img791.png)
|
andres
2014-09-09
 , we use Eq. (7.2).
The plastic moment
, we use Eq. (7.2).
The plastic moment 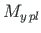 about the neutral axis y in a plastic hinge
can be computed from Eq. (7.3).
about the neutral axis y in a plastic hinge
can be computed from Eq. (7.3).
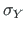 is the yield stress,
is the yield stress,
 - an area in tension,
- an area in tension,
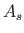 - an area in compression.
- an area in compression.
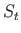 and
and 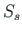 are accordingly the first moment of the area in tension and that of the area in compression about neutral axis.
are accordingly the first moment of the area in tension and that of the area in compression about neutral axis.
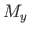 are shown in Fig. 7.4 h.
are shown in Fig. 7.4 h.