Next: 6. The EST method Up: 5.3 Solutions of a Previous: 5.3.3 The particular solution
Let 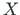 ,
, 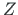 be the global coordinate system (see Fig. 5.5),
be the global coordinate system (see Fig. 5.5), 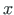 ,
, 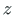 the local (initial) coordinate system, and
the local (initial) coordinate system, and
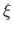 ,
, 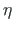 the current coordinate system [Yaw09].
the current coordinate system [Yaw09].
We have derived the transfer matrix
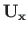 from Eq. (5.90) for the normal force N and shear force
from Eq. (5.90) for the normal force N and shear force 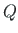 shown in Fig. 5.1.
These forces (N,
shown in Fig. 5.1.
These forces (N, 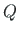 ) we bind with the current coordinate system (
) we bind with the current coordinate system (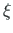 ,
, 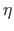 ).
).
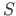 and transverse shear force
and transverse shear force 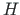 are described in the initial (local) coordinate system (
are described in the initial (local) coordinate system (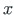 ,
, 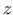 ).
In the global coordinate system (
).
In the global coordinate system (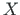 ,
, 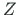 ), the joint equilibrium equations are written.
), the joint equilibrium equations are written.
We now consider a symbolic matrix transfer equation at the axial force S and Sign Convention 2:
In order to change variables 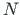 ,
,  to
to 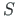 ,
, 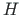 , we will need the transformation relations of Eq. (5.101) [Krä91b]:
, we will need the transformation relations of Eq. (5.101) [Krä91b]:
To compute the transformation matrix
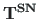 , the GNU Octave function
ytransf.m
(p.
, the GNU Octave function
ytransf.m
(p. ![]() ) can be used.
) can be used.
We will make the inverse change of variables 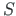 ,
, 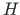 to
to 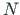 ,
, 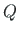 with the equations
with the equations
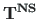 can be computed using the GNU Octave function
ytransfp.m
(p.
can be computed using the GNU Octave function
ytransfp.m
(p.
The matrix
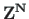 has the inverse matrix
has the inverse matrix
 , i.e
, i.e
 :
:
When comparing equations (5.96) and (5.107), we show that
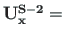
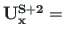
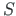 ,
,  ; Sign Convention 2)
; Sign Convention 2)
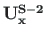 of Eq. (5.110) and
of Eq. (5.110) and
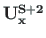 of Eq. (5.111) can be computed using the GNU Octave function
ylfmhvII.m
,
taking the input argument
of Eq. (5.111) can be computed using the GNU Octave function
ylfmhvII.m
,
taking the input argument  equal to 1.0
(
equal to 1.0
( is input for scaling multiplier
is input for scaling multiplier 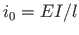 , see p.
, see p.
If we multiply the loading vectors of Eqs. (5.92) and (5.93)
(for the normal and shear forces 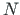 ,
, 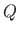 ) from left by
) from left by
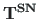 (see Eq. (5.109)),
we get the products of Eqs. (5.112) and (5.113)
(for the axial and transverse shear forces
(see Eq. (5.109)),
we get the products of Eqs. (5.112) and (5.113)
(for the axial and transverse shear forces 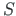 ,
, 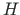 ):
):
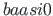 equal to 1.0
(
equal to 1.0
(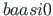 is input for the scaling multiplier
is input for the scaling multiplier  , see p.
, see p.
Multiplying the loading vectors of Eqs. (5.94) and (5.95)
(for the normal and shear forces 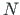 ,
, 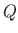 ) from left by
) from left by
 (see Eq. (5.109)),
we get the products of Eqs. (5.114) and (5.115)
(for the axial and transverse shear forces
(see Eq. (5.109)),
we get the products of Eqs. (5.114) and (5.115)
(for the axial and transverse shear forces  ,
, 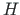 ):
):
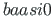 equal to 1.0
(
equal to 1.0
(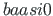 is input for the scaling multiplier
is input for the scaling multiplier 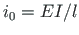 , see p.
, see p.