Next: III. Plastic analysis of Up: 6. The EST method Previous: 6.2 Illustrative frame problem
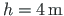 is shown. Two spans of the frame are of the same length,
is shown. Two spans of the frame are of the same length,
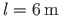 .
The beam of the first span carries a uniform load
.
The beam of the first span carries a uniform load
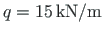 .
The rightmost column is loaded with horizontal concentrated loads
.
The rightmost column is loaded with horizontal concentrated loads
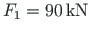 and
and
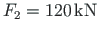 . Each of the frame columns carries a vertical concentrated load
. Each of the frame columns carries a vertical concentrated load
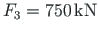 .
.
Let us assume that the value of the column flexural rigidity
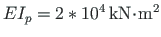 and beam flexural rigidity
and beam flexural rigidity
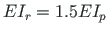 ; axial rigidity of the columns
; axial rigidity of the columns
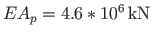 and that of the beam
and that of the beam
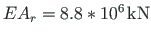 ; shear rigidity of the columns
; shear rigidity of the columns
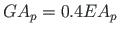 and that of the beam
and that of the beam
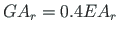 .
.
We wish to compute the displacements, reactions, internal forces, and draw the axial force, shear force and bending moment diagrams.
Problem Solving. We use the EST method to solve the problem. The solving procedure includes the following.
1. Input data for the GNU Octave program yspESTframe2LaheWFI.m are shown in excerpt from the program: element and nodal loads - excerpt 6.5; nodal coordinates -excerpt 6.6; element properties, topology and hinges - excerpt 6.7.
epsdountil=0.0000001; # for iteration (max |S| increment) Number_of_frame_nodes=6 Number_of_elements=5 Number_of_support_reactions=8 spNNK=12*Number_of_elements+Number_of_support_reactions; Number_of_unknowns=spNNK Displacements and forces are calculated on parts ''Nmitmeks'' of the element Nmitmeks=4 Lp=12.0; # graphics axis # --- Element properties ---
EIp=20000 # kN/m^2 EIr=40000 # kN/m^2 EAp=4.6*10^6 #EAp=4.6*10^15; EAr=6.8*10^6; #EAr=6.8*10^15 GAp=0.4*EAp; GAr=0.4*EAr; |
baasi0=EIp/5.6 # scaling multiplier for the displacements #baasi0=1.0; #Element load in local coordinates # qz qx qA qL # Uniformly distributed load in local coordinate z and x directions LoadsqONelement=4; esQkoormus=zeros(LoadsqONelement,4,ElementideArv);
esQkoormus(1,1:4,1)=[0.0 0.0 0.0 4.0]; esQkoormus(1,1:4,2)=[15.0 0.0 0.0 6.0]; esQkoormus(1,1:4,3)=[0.0 0.0 0.0 4.0]; esQkoormus(1,1:4,4)=[0.0 0.0 0.0 6.0]; esQkoormus(1,1:4,5)=[0.0 0.0 0.0 4.0];
# # Point load in local coordinate z and x directions kN # Fz, Fx, aF (coordinate of the point of force application) LoadsF_on_Element=5; esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);
esFjoud(1,1:3,1)=[0.0 0.0 4.0]; esFjoud(1,1:3,2)=[0.0 0.0 6.0]; esFjoud(1,1:3,3)=[0.0 0.0 4.0]; esFjoud(1,1:3,4)=[0.0 0.0 6.0]; esFjoud(1,1:3,5)=[120.0 0.0 2.0];
# # Node forces in global coordinates # sSolmF(forces,1,nodes); forces=[Fx; Fz; My] sSolmF = zeros(3,1,SolmedeArv);
#sSolmF(:,1,1)= 0.0 sSolmF(2,1,2)= 750.0; % Fz #sSolmF(:,1,3)= 0.0 sSolmF(2,1,4)= 750.0; % Fz #sSolmF(:,1,5)= 0.0 sSolmF(1,1,6)= -90.0; % Fx sSolmF(2,1,6)= 750.0; % Fz
# #s1F(1,1,1)=0.0; # force Fz #s1F(2,1,1)=0.0; # force Fz #s1F(3,1,1)=0.0; # force My # Support shift - tSiire# # Support shift is multiplied by scaling multiplier tSiire = zeros(3,1,SolmedeArv);
#tSiire(:,1,1)= 0.0 #tSiire(2,1,1)= 0.01*baasi0 #tSiire(:,1,2)= 0.0 #tSiire(:,1,3)= 0.0 #tSiire(:,1,4)= 0.0 #tSiire(:,1,5)= 0.0 #tSiire(:,1,6)= 0.0
#==========
# Nodal coordinates
#==========
krdn=[# x z
0.0 0.0; % node 1
0.0 -4.0; % node 2
6.0 0.0; % node 3
6.0 -4.0; % node 4
12.0 0.0; % node 5
12.0 -4.0]; %% node 6
#==========
#
#==========
# Restrictions on support displacements (on - 1, off - 0)
# Support No u w fi
#==========
tsolm=[1 1 1 0; % node 1
3 1 1 1; % node 3
5 1 1 1]; % node 5
#==========
# ------------- Element properties, topology and hinges --------- elasts=[# Element properties # n2 - end of the element # n1 - beginning of the element # N, Q, M - hinges at the end of the element # N, Q, M - hinges at the beginning of the element # EIp EAp GAp 2 1 0 0 0 0 0 1; % element 1 EIr EAr GAr 4 2 0 0 0 0 0 0; % element 2 EIp EAp GAp 4 3 0 0 0 0 0 0; % element 3 EIr EAr GAr 6 4 0 0 0 0 0 1; % element 4 EIp EAp GAp 5 6 0 0 0 0 0 0]; % element 5 # 1 - hinge 'true' (axial, shear, moment hinges) #
2. Assembling and solving the boundary problem equations (6.5), carried out by the function Lahe2FrameDFIm(baasi0,Ntoerkts,esQkoormus,esFjoud,sSolmF,tsolm,tSiire, krdn,selem). The program has numbered the displacements and forces of the element ends of the frames as shown in Figs. 6.2 and 6.8.
The results of iteration of the axial forces are given in excerpt 6.7 from the computing diary.
SIvec = Element Linear 1 2 3 4 1 -824.978 -828.823 -828.821 -828.821 -828.821 2 -25.760 -21.535 -21.499 -21.499 -21.499 3 -775.104 -773.182 -773.186 -773.186 -773.186 4 -79.661 -77.786 -77.769 -77.769 -77.769 5 -739.918 -737.994 -737.993 -737.993 -737.993
The unscaled initial parameter vectors of the elements are shown in excerpt 6.8 from the computing diary.
-------- Scaling multiplier for displacements = 1/baasi0 -------- ============================================================================ Unscaled initial parameter vector Element No u w fi S H M ---------------------------------------------------------------------------- 1 -0.000e+00 0.000e+00 1.166e-02 828.821 21.499 0.000 2 -3.056e-02 7.207e-04 -1.311e-04 21.499 -78.821 111.330 3 -0.000e+00 0.000e+00 0.000e+00 773.186 56.270 -157.134 4 -3.058e-02 6.723e-04 -2.423e-03 77.769 -12.007 0.000 5 6.417e-04 3.065e-02 4.838e-03 737.993 12.231 -72.037 ----------------------------------------------------------------------------
The support reactions of the frame in global coordinates are shown in excerpt 6.9 from the computing diary.
Support reactions begin from X row: 61
===========================================
No X Node Cx <=> 1
Cz <=> 2
Cy <=> 3
-------------------------------------------
61 +2.149932e+01 1 1
62 -8.288206e+02 1 2
63 +5.626986e+01 3 1
64 -7.731859e+02 3 2
65 -1.571336e+02 3 3
66 +1.322308e+02 5 1
67 -7.379935e+02 5 2
68 -2.395078e+02 5 3
--------------------------------------------
3. Output: the element displacements and forces determined by the transfer matrix are given in excerpt 6.10 from the computing diary.
The horizontal displacements diagram of the frame EST2 is depicted
in Fig. 6.9.
The bending moment M, shear force Q and axial force N diagrams of the frame EST2 are shown
in Fig. 6.10.
![\includegraphics[width=105mm]{joonised/hor_ii3e.eps}](img741.png)
|
| (bracketed are values of linear solution) |
![\includegraphics[width=115mm]{joonised/nep_ii3e.eps}](img742.png) [Axial force N diagram] | ||
![\includegraphics[width=125mm]{joonised/qep_ii3e.eps}](img743.png) [Shear force Q diagram] |
![\includegraphics[width=125mm]{joonised/mom_ii3e.eps}](img744.png) [Bending moment diagram] | (bracketed are values of linear solution) |
#================================================================================= Element displacements and forces determined by transfer matrix #================================================================================= Displacements and forces of element no 1 of length 4.000 m The element is divided into 4 parts displacement u - 0.00000e+00 -1.80178e-04 -3.60357e-04 -5.40535e-04 -7.20714e-04 displacement w - 0.00000e+00 -1.14016e-02 -2.12611e-02 -2.81000e-02 -3.05647e-02 rotation fi - 1.16608e-02 1.08844e-02 8.58719e-03 4.86412e-03 -1.31089e-04 normal force N - -828.82062 -828.82062 -828.82062 -828.82062 -828.82062 shear force Q - -31.16401 -30.52051 -28.61656 -25.53080 -21.39067 moment force M - 0.00000 -30.94922 -60.62029 -87.78785 -111.32995 ------------------ axial force S - -828.82062 -828.82062 -828.82062 -828.82062 -828.82062 transv force H - -21.49932 -21.49932 -21.49932 -21.49932 -21.49932 ---------------------------------------------------------------------------- Displacements and forces of element no 2 of length 6.000 m The element is divided into 4 parts displacement u - -3.05647e-02 -3.05695e-02 -3.05742e-02 -3.05789e-02 -3.05837e-02 displacement w - 7.20714e-04 3.71930e-03 7.67193e-03 7.50247e-03 6.72336e-04 rotation fi - -1.31089e-04 -3.02184e-03 -1.68423e-03 2.19229e-03 6.91421e-03 normal force N - -21.49932 -21.49932 -21.49932 -21.49932 -21.49932 shear force Q - 78.82344 56.38559 33.85683 11.27349 -11.32803 moment force M - -111.32995 -9.90955 57.78135 91.63364 91.59272 ------------------ axial force S - -21.49932 -21.49932 -21.49932 -21.49932 -21.49932 transv force H - 78.82062 56.32062 33.82062 11.32062 -11.17938 ---------------------------------------------------------------------------- Displacements and forces of element no 3 of length 4.000 m The element is divided into 4 parts displacement u - 0.00000e+00 -1.68084e-04 -3.36168e-04 -5.04252e-04 -6.72336e-04 displacement w - 0.00000e+00 -3.44769e-03 -1.17895e-02 -2.18995e-02 -3.05837e-02 rotation fi - 0.00000e+00 6.40393e-03 9.75665e-03 9.92896e-03 6.91421e-03 normal force N - -773.18589 -773.18589 -773.18589 -773.18589 -773.18589 shear force Q - -56.26986 -61.22129 -63.81357 -63.94679 -61.61583 moment force M - 157.13359 98.19802 35.47841 -28.60837 -91.59272 ------------------ axial force S - -773.18589 -773.18589 -773.18589 -773.18589 -773.18589 transv force H - -56.26986 -56.26986 -56.26986 -56.26986 -56.26986 ---------------------------------------------------------------------------- Displacements and forces of element no 4 of length 6.000 m The element is divided into 4 parts displacement u - -3.05837e-02 -3.06008e-02 -3.06180e-02 -3.06351e-02 -3.06523e-02 displacement w - 6.72336e-04 4.07754e-03 6.11281e-03 5.41621e-03 6.41733e-04 rotation fi - -2.42253e-03 -1.96544e-03 -5.96843e-04 1.67528e-03 4.83769e-03 normal force N - -77.76918 -77.76918 -77.76918 -77.76918 -77.76918 shear force Q - 12.19491 12.15936 12.05292 11.87622 11.63028 moment force M - 0.00000 18.27458 36.44263 54.39821 72.03667 ------------------ axial force S - -77.76918 -77.76918 -77.76918 -77.76918 -77.76918 transv force H - 12.00651 12.00651 12.00651 12.00651 12.00651 ---------------------------------------------------------------------------- Displacements and forces of element no 5 of length 4.000 m The element is divided into 4 parts displacement u - 6.41733e-04 4.81300e-04 3.20867e-04 1.60433e-04 0.00000e+00 displacement w - 3.06523e-02 2.41507e-02 1.49071e-02 4.86941e-03 -6.63532e-15 rotation fi - 4.83769e-03 8.02360e-03 1.03047e-02 8.60626e-03 5.15213e-15 normal force N - -737.99349 -737.99349 -737.99349 -737.99349 -737.99349 shear force Q - -15.80100 -18.15219 -139.83562 -138.58218 -132.23082 moment force M - 72.03667 55.00768 35.95515 -103.68339 -239.50781 ------------------ axial force S - -737.99349 -737.99349 -737.99349 -737.99349 -737.99349 transv force H - -12.23082 -12.23082 -132.23082 -132.23082 -132.23082 ----------------------------------------------------------------------------
Testing a static equilibrium for the frame
Consider next a static equilibrium of the frame shown in Fig. 6.11.
Let us project the forces onto the X-axis (see Fig. 6.11),
and onto the Z-axis,
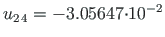 (see excerpt 6.10 from the computing diary). The additional moment
(see excerpt 6.10 from the computing diary). The additional moment 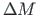 from node (member) displacements
from node (member) displacements
Table 6.1 gives the values for internal reactions 6.1 6.2 6.3 (contact forces 6.4)
determined by the EST method.
These can be compared with the results (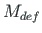 ) 6.6 obtained with the slope-deflection method.
The table describes the boundary values (internal reactions) after the second iteration, whereas those in table 16.17 of [Lah12] had been obtained in the first iteration.
) 6.6 obtained with the slope-deflection method.
The table describes the boundary values (internal reactions) after the second iteration, whereas those in table 16.17 of [Lah12] had been obtained in the first iteration.
| Element | Linear theory | 2nd order theory | |||||
| No | 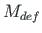
|
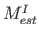
|
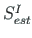
|
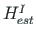
|
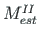
|
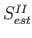
|
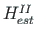
|
![$\left[\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m} \right]$](img766.png)
|
![$\left[\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m} \right]$](img1129xx.png)
|
![$\left[\mathrm{kN}\right]$](img1130xx.png)
|
![$\left[\mathrm{kN}\right]$](img1131xx.png)
|
![$\left[\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m} \right]$](img1132xx.png)
|
![$\left[\mathrm{kN}\right]$](img1133xx.png)
|
![$\left[\mathrm{kN}\right]$](img1134xx.png)
|
|
| 1 begin. | 0.0000 | 0.000 | 824.978 | 25.760 | 0.000 | 828.820 | 21.499 |
| 1 end | -103.1977 | -103.040 | -824.978 | -25.760 | -111.330 | -828.820 | -21.499 |
| 2 begin. | 103.1977 | 103.040 | 25.760 | -74.978 | 111.330 | 21.499 | -78.820 |
| 2 end | 76.9767 | 76.829 | -25.760 | -15.022 | 91.593 | -21.499 | -11.179 |
| 3 begin. | -138.8954 | -138.774 | 775.104 | 53.901 | -157.133 | 773.186 | 56.270 |
| 3 end | -76.9767 | -76.829 | -775.104 | -53.901 | -91.593 | -773.186 | -56.270 |
| 4 begin. | 0.0000 | 0.000 | 79.661 | -10.082 | 0.000 | 77.769 | -12.007 |
| 4 end | 60.3488 | 60.490 | -79.661 | 10.082 | 72.037 | -77.769 | 12.001 |
| 5 begin. | -60.3488 | -60.490 | 739.918 | 10.339 | -72.037 | 737.993 | 12.231 |
| 5 end | -220.5814 | -220.868 | -739.918 | -130.339 | -239.508 | -737.993 | -132.231 |
The boundary value problem (differential equations together with a set of boundary conditions) is well posed with the EST method.