Next: 6.2 Illustrative frame problem Up: 6. The EST method Previous: 6. The EST method
Consider solving a boundary value problem with the EST method. The second-order analysis is a nonlinear problem and the superposition of deflections cannot be applied. Axial forces are generally not known at the outset of a frame analysis. A set of axial forces of the frame members is determined as a linear structure. At the second iteration, the axial forces from the first iteration are used. If the axial forces obtained by the second iteration differ greatly from the values of the first iteration, the calculated values are used to find new values and the analysis is repeated.
As can be seen from the computing diary excerpt 6.1, the axial forces of the frame elements (given in Fig. 6.7), obtained in the third iteration, do not differ from the values of the second iteration.
SIvec =
Linear 1 2 3 4
1 -824.978 -828.823 -828.821 -828.821 -828.821
2 -25.760 -21.535 -21.499 -21.499 -21.499
3 -775.104 -773.182 -773.186 -773.186 -773.186
4 -79.661 -77.786 -77.769 -77.769 -77.769
5 -739.918 -737.994 -737.993 -737.993 -737.993
In excerpt 6.2 from the computing diary, an iteration for the support reactions of the frame from Fig. 6.7 is shown.
Support_Reactions =
Linear 1 2 3 4
Cx 25.760 21.535 21.499 21.499 21.499
Cz -824.978 -828.823 -828.821 -828.821 -828.821
Cx 53.901 56.251 56.270 56.270 56.270
Cz -775.104 -773.182 -773.186 -773.186 -773.186
Cy(moment) -138.774 -157.125 -157.134 -157.134 -157.134
Cx 130.339 132.214 132.231 132.231 132.231
Cz -739.918 -737.994 -737.993 -737.993 -737.993
Cy(moment) -220.868 -239.506 -239.508 -239.508 -239.508
|
|
Let us start by assembling a system of non-symmetric sparse equations
This collection of boundary problem equations (6.1) is assembled
and solved by the GNU Octave function Lahe2FrameDFIm.m
(p. ![]() ).
).
The basic equations of a frame are defined as
 and
and
 are expressed as
are expressed as
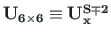 is the transfer matrix given with Eqs. (5.110) and
(5.111) at
is the transfer matrix given with Eqs. (5.110) and
(5.111) at 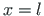 (Sign Convention 2);
(Sign Convention 2);
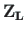 ,
,
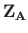 are the vectors of displacements and forces
at the end and at the beginning of the element, respectively; the loading vector
are the vectors of displacements and forces
at the end and at the beginning of the element, respectively; the loading vector
 is given with Eqs. (5.112), (5.113), (5.114), and (5.115);
is given with Eqs. (5.112), (5.113), (5.114), and (5.115);
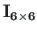 is a unit matrix
is a unit matrix 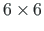 for the frame element.
for the frame element.
Equilibrium equations at beam joints and joint equilibrium equations are discussed in sections 2.2 and 2.3, side conditions and restrictions on support displacements are dealt with in sections 2.4 and 2.5.
Inserting the system of the basic equations (6.2) into the system Eq. (6.1) is shown in excerpt 6.1 of the program.
andres