4.3 Illustrative truss problem

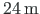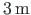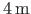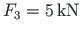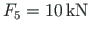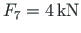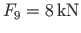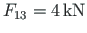Example 4.3 Problem Statement. Determine the forces in the truss shown in Fig. 4.12. The truss of length $24{\,}\mathrm{m}$ , panel length $3{\,}\mathrm{m}$ , and height $4{\,}\mathrm{m}$ is loaded at bottom chord nodes by vertical forces $F_{3} = 5{\,}\mathrm{kN}$ , $F_{5} = 10{\,}\mathrm{kN}$ , $F_{7} = 4{\,}\mathrm{kN}$ , $F_{9} = 8{\,}\mathrm{kN}$ , $F_{13} = 4{\,}\mathrm{kN}$ , $F_{15} = 8{\,}\mathrm{kN}$ .

**Figure 4.12:** A polygonal eight-panel truss
$\includegraphics[width=135mm]{joonised/mjnait0.eps}$

We wish to compute the reactions, internal forces 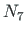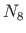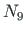$N_{7}$ , $N_{8}$ , $N_{9}$ , and $N_{10}$ , and draw influence line diagrams for the truss members 7, 8, 9, and 10.

Problem Solving. To solve the problem, the EST method is employed. For assembling and solving the boundary problem equation

$\displaystyle \mathbf{spA}{\cdot}\mathbf{Z} = \mathbf{B}$

(4.8)

the GNU Octave program spESTtrussN2.m is used.

1. Input data for this program are shown in excerpts from the program: element and nodal loads - excerpt 4.7; nodal coordinates - excerpt 4.8; topology and hinges - excerpt 4.9.

Program excerpt 4.7 ( spESTtrussN2.m )

 Number_of_truss_nodes=16
 Number_of_elements=29
 Number_of_support_reactions=3
 spNNK=Number_of_elements+Number_of_support_reactions;
 Number_of_unknowns=spNNK 
 Lp=24.0; # graphics axes 
# --- Truss properties ---

  
 d=3.0;     # panel length
 Npanel=8;  # number of panels
 L=24.0;    # truss span
 H=4.0;     # truss height
 jaotT=L/8;

# ---- load variants -----
load_variant=1;
#load_variant=2
#load_variant=3

 
switch (koormusvariant)
case{1}
disp(' Load variant 1 ')
#
#==========
mjNr1=5;  # influence line diagram numbers 
mjNr2=2;
mjNr3=4;
mjNr4=7;
mjNr5=9;
#==========

#==========
# Node forces in global coordinates
#==========
VJoud=[# Fx    Fz

         0     0;    # node 1
         0     0;    # node 2
         0     5;    # node 3
         0     0;    # node 4
         0    10;    # node 5
         0     0;    # node 6
         0     4;    # node 7
         0     0;    # node 8
         0     8;    # node 9
         0     0;    # node 10
         0     0;    # node 11
         0     0;    # node 12
         0     4;    # node 13
         0     0;    # node 14
         0     8;    # node 15
         0     0];   # node 16

#========== # Unit load acting at nodes #========== YJoudS=[# Fx Fz

          0     1;    # node 1
          0     0;    # node 2
          0     1;    # node 3
          0     0;    # node 4
          0     1;    # node 5
          0     0;    # node 6
          0     1;    # node 7
          0     0;    # node 8
          0     1;    # node 9
          0     0;    # node 10
          0     1;    # node 11
          0     0;    # node 12
          0     1;    # node 13
          0     0;    # node 14
          0     1;    # node 15
          0    1];    # node 16

# case{2} disp(' Load variant 2 ') # case{3} disp(' Load variant 3 ') # otherwise disp(' No load variant cases ') endswitch #

Program excerpt 4.8 ( spESTtrussN2.m )
#========== # Nodal coordinates #========== krdn=[# x z

        0.0       0.0;    # node 1
        3.0      -2.4;    # node 2
        3.0       0.0;    # node 3
        6.0      -3.6;    # node 4
        6.0       0.0;    # node 5
        9.0      -4.0;    # node 6
        9.0       0.0;    # node 7
       12.0      -4.0;    # node 8
       12.0       0.0;    # node 9
       15.0      -4.0;    # node 10
       15.0       0.0;    # node 11
       18.0      -3.6;    # node 12
       18.0       0.0;    # node 13
       21.0      -2.4;    # node 14
       21.0       0.0;    # node 15
       24.0       0.0];   # node 16

#========== # Restrictions on support displacements (on - 1, off - 0) # Support u w #========== tsolm=[# x z

         1     1;    # node 1
         0     0;    # node 2
         0     0;    # node 3
         0     0;    # node 4
         0     0;    # node 5
         0     0;    # node 6
         0     0;    # node 7
         0     0;    # node 8
         0     0;    # node 9
         0     0;    # node 10
         0     0;    # node 11
         0     0;    # node 12
         0     0;    # node 13
         0     0;    # node 14
         0     0;    # node 15
         0     1];   # node 16

Program excerpt 4.9 ( spESTtrussN2.m )
#========== #----- Element topology ------ #========== selemjl=[# n1 - beginning of the element # n2 - end of the element

           1   2;    # element 1
           2   3;    # element 2
           1   3;    # element 3
           2   4;    # element 4
           2   5;    # element 5
           3   5;    # element 6
           4   5;    # element 7
           4   6;    # element 8
           5   6;    # element 9
           5   7;    # element 10
           6   7;    # element 11
           6   8;    # element 12
           6   9;    # element 13
           7   9;    # element 14
           8   9;    # element 15
           8  10;    # element 16
           9  10;    # element 17
          10  13;    # element 18
           9  11;    # element 19
          10  12;    # element 20
          10  11;    # element 21
          11  13;    # element 22
          12  13;    # element 23
          12  14;    # element 24
          13  14;    # element 25
          13  15;    # element 26
          14  15;    # element 27
          14  16;    # element 28
          15  16];   # element 29

The procedure for computing the internal forces in truss members is discussed in [Lah12].

3. Output: the internal forces of elements given in excerpt 4.7 from the computing diary.

Computing diary excerpt 4.7 (load case 1 spESTtrussN2.m )
========================================= Internal forces in truss members The last 3 forces are support reactions No N -----------------------------------------

 
   1   -32.6157
   2     5.0000
   3    25.4686
   4   -32.0864
   5     5.5361
   6    25.4686
   7     7.9445
   8   -30.0552
   9    -1.7536
  10    30.8438
  11     4.0000
  12   -31.8750
  13     1.7187
  14    30.8438
  15    -0.0000
  16   -31.8750
  17     8.2813
  18    -4.2189
  19    26.9063
  20   -24.5906
  21     0.0000
  22    26.9063
  23     6.5000
  24   -26.2525
  25     1.4008
  26    23.2811
  27     8.0000
  28   -29.8143
  29    23.2811
  30     0.0000
  31   -20.3750
  32   -18.6250

In excerpt 4.8 from the computing diary, the influence line ordinates are for the members belonging to the lower chord. The procedure for computing the influence line ordinates is discussed in [KW90] and [Lah12].
The influence line diagram of member 9 is shown in Fig. 4.13.

Figure 4.13: Influence line for member 9

$\includegraphics[width=0.80\textwidth]{joonised/MojujoonN9.eps}$

Computing diary excerpt 4.8 ( spESTtrussN2.m )
===================================================== Influence line x-coordinates ----------------------------------------------------- 0 3 6 9 12 15 18 21 24 -----------------------------------------------------
===================================================== Influence line ordinates The last 3 rows are for support reactions ----------------------------------------------------- 1 0.0000 -1.4007 -1.2006 -1.0005 -0.8004 -0.6003 -0.4002 -0.2001 0.0000 2 0.0000 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 3 0.0000 1.0937 0.9375 0.7812 0.6250 0.4687 0.3125 0.1562 0.0000 4 0.0000 -0.6731 -1.3463 -1.1219 -0.8975 -0.6731 -0.4488 -0.2244 0.0000 5 0.0000 -0.6003 0.4002 0.3335 0.2668 0.2001 0.1334 0.0667 0.0000 6 0.0000 1.0937 0.9375 0.7812 0.6250 0.4687 0.3125 0.1562 0.0000 7 0.0000 0.1667 0.3333 0.2778 0.2222 0.1667 0.1111 0.0556 0.0000 8 0.0000 -0.6305 -1.2611 -1.0509 -0.8407 -0.6305 -0.4204 -0.2102 0.0000 9 0.0000 0.2604 0.5208 -0.6076 -0.4861 -0.3646 -0.2431 -0.1215 0.0000 10 0.0000 0.4688 0.9375 1.4063 1.1250 0.8438 0.5625 0.2813 0.0000 11 0.0000 0.0000 0.0000 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 12 0.0000 -0.3750 -0.7500 -1.1250 -1.5000 -1.1250 -0.7500 -0.3750 0.0000 13 -0.0000 -0.1563 -0.3125 -0.4688 0.6250 0.4688 0.3125 0.1563 0.0000 14 0.0000 0.4688 0.9375 1.4063 1.1250 0.8438 0.5625 0.2813 0.0000 15 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 16 0.0000 -0.3750 -0.7500 -1.1250 -1.5000 -1.1250 -0.7500 -0.3750 0.0000 17 0.0000 0.1563 0.3125 0.4688 0.6250 -0.4688 -0.3125 -0.1563 0.0000 18 0.0000 -0.1215 -0.2431 -0.3646 -0.4861 -0.6076 0.5208 0.2604 0.0000 19 0.0000 0.2813 0.5625 0.8438 1.1250 1.4063 0.9375 0.4688 0.0000 20 0.0000 -0.2102 -0.4204 -0.6305 -0.8407 -1.0509 -1.2611 -0.6305 0.0000 21 0.0000 0.0000 0.0000 0.0000 0.0000 1.0000 0.0000 0.0000 0.0000 22 0.0000 0.2813 0.5625 0.8438 1.1250 1.4063 0.9375 0.4688 0.0000 23 0.0000 0.0556 0.1111 0.1667 0.2222 0.2778 0.3333 0.1667 0.0000 24 0.0000 -0.2244 -0.4488 -0.6731 -0.8975 -1.1219 -1.3463 -0.6731 0.0000 25 0.0000 0.0667 0.1334 0.2001 0.2668 0.3335 0.4002 -0.6003 0.0000 26 0.0000 0.1562 0.3125 0.4687 0.6250 0.7812 0.9375 1.0937 0.0000 27 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 1.0000 0.0000 28 0.0000 -0.2001 -0.4002 -0.6003 -0.8004 -1.0005 -1.2006 -1.4007 0.0000 29 0.0000 0.1562 0.3125 0.4687 0.6250 0.7812 0.9375 1.0937 0.0000 30 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 31 -1.0000 -0.8750 -0.7500 -0.6250 -0.5000 -0.3750 -0.2500 -0.1250 0.0000 32 0.0000 -0.1250 -0.2500 -0.3750 -0.5000 -0.6250 -0.7500 -0.8750 -1.0000 -----------------------------------------------------

The sparsity pattern of matrix spA of the polygonal truss is given in Fig. 4.14.

Figure 4.14: Sparsity pattern of matrix spA of the polygonal truss

$\includegraphics[width=0.70\textwidth]{joonised/spTruss_h6remaatriks.eps}$