4.2 Illustrative beam problem

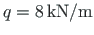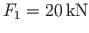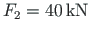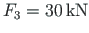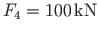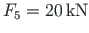Example 4.2 Problem Statement. Given is the Gerber beam shown in Fig. 4.7. The beam is loaded with a uniform load $q = 8{\,}\mathrm{kN/m}$ and with concentrated forces $F_{1} = 20{\,}\mathrm{kN}$ , $F_{2} = 40{\,}\mathrm{kN}$ , $F_{3} = 30{\,}\mathrm{kN}$ , $F_{4} = 100{\,}\mathrm{kN}$ , $F_{5} = 20{\,}\mathrm{kN}$ .

**Figure 4.7:** The three-span Gerber beam EST
$\includegraphics[width=140mm]{joonised/talaEST323Ax.eps}$

We wish to compute the reactions and internal forces, and draw the shear force and bending moment diagrams.

Problem Solving. To solve the problem, the EST method is used. The solving procedure includes the following.

Data input: the number of beam nodes, elements, support reactions; element loads in local coordinates, node forces in global coordinates, nodal coordinates, topology and hinges.

$\displaystyle \mathbf{spA}{\cdot}\mathbf{Z} = \mathbf{B}$ (4.5)
Assembling and solving the boundary problem equations (4.5) (prepared and solved by the program):
1. writing the basic equations of beam in transfer matrix form,
2. adding the joint equilibrium equations,
3. adding the side conditions (hinges),
4. solving the system of sparse equations,
5. producing an output: initial parameter vectors for element forces; support reactions.
Output: element forces determined by the transfer matrix.

1. Input data for the GNU Octave program spESTGerberBeamQM.m are shown in excerpts from the program: element and nodal loads - excerpt 4.4; nodal coordinates - excerpt 4.5; element properties, topology and hinges - excerpt 4.6.

Program excerpt 4.4 ( spESTGerberBeamQM.m )

 Number_of_frame_nodes=8
 Number_of_elements=7
 Number_of_support_reactions=5
 spNNK=4*Number_of_elements+Number_of_support_reactions;
 Number_of_unknowns=spNNK 
 Forces are calculated on parts ("Nmitmeks") of the element  
 Nmitmeks=4
 Lp=31.0; # graphics axes
# --- Element loads ---

  
F1=20;
F2=40;
F3=30;
F4=100;
F5=20;
qz=8.0;
## ---- load variants -----
load_variant=1
#load_variant=2
#load_variant=3

switch (koormusvariant) case{1} disp(' Load variant 1 ')
#Element load in local coordinates # qz qA qL # Uniformly distributed load in local coordinate z direction LoadsqONelement=4; esQkoormus=zeros(LoadsqONelement,3,ElementideArv);

esQkoormus(1,1:3,1)=[0.0 0.0 4.0];
esQkoormus(1,1:3,2)=[qz 0.0 8.0];
esQkoormus(1,1:3,3)=[qz 0.0 2.0];
esQkoormus(1,1:3,4)=[qz 0.0 6.0];
esQkoormus(1,1:3,5)=[0.0 0.0 2.0];
esQkoormus(1,1:3,6)=[0.0 0.0 8.0];
esQkoormus(1,1:3,7)=[0.0 0.0 1.0];

# Point load in local coordinate z direction kN # Fz, aF (coordinate of the point of force application) LoadsF_on_Element=5; esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);

esFjoud(1,1:2,1)=[0.0 4.0];
esFjoud(1,1:2,2)=[F2 4.0];
esFjoud(1,1:2,3)=[0.0 2.0]; 
esFjoud(1,1:2,4)=[F3 2.0];
esFjoud(1,1:2,5)=[0.0 2.0]; 
esFjoud(1,1:2,6)=[F4 4.0];
esFjoud(1,1:2,7)=[0.0 1.0];

#Node forces in global coordinates # sSolmF(forces,1,nodes); forces=[Fz; My] sSolmF = zeros(2,1,SolmedeArv);

#sSolmF(:,1,1)= 0.0;
sSolmF(1,1,2)= 20.0;
#sSolmF(:,1,3)= 0.0;
#sSolmF(:,1,4)= 0.0
#sSolmF(:,1,5)= 0.0
#sSolmF(:,1,6)= 0.0
#sSolmF(:,1,7)= 0.0
sSolmF(1,1,8)= 20.0;
#%disp(' Kustuta ')
     s1F(:,:) = sSolmF(:,1,1);
     s2F(:,:) = sSolmF(:,1,2);
     s3F(:,:) = sSolmF(:,1,3);
     s4F(:,:) = sSolmF(:,1,4);
     s5F(:,:) = sSolmF(:,1,5);
     s6F(:,:) = sSolmF(:,1,6);
     s7F(:,:) = sSolmF(:,1,7);
     s8F(:,:) = sSolmF(:,1,8);

#s1F(1,1,1)=0.0; # force Fz #s1F(2,1,1)=0.0; # force My
case{2} disp(' Load variant 2 ') case{3} disp(' Load variant 3 ') # otherwise disp(' No load variant cases ') endswitch

**Figure 4.8:** Numeration of displacements and forces of the Gerber beam
$\includegraphics[width=1.0\textwidth]{joonised/talaEST323Axnumbr.eps}$

Program excerpt 4.5 ( spESTGerberBeamQM.m )
#========== # Nodal coordinates #========== krdn=[# x 0.0 ; # node 1 4.0 ; # node 2 12.0 ; # node 3 14.0 ; # node 4 20.0 ; # node 5 22.0 ; # node 6 30.0 ; # node 7 31.0 ]; # node 8 #========== # Restrictions on support displacements (on - 1, off - 0) # Support No w fi #========== tsolm=[1 1 1 ; # node 1 3 1 0 ; # node 2 6 1 0 ; # node 3 7 1 0 ]; # node 4 #==========

Program excerpt 4.6 ( spESTGerberBeamQM.m )
# ------------- Element properties, topology and hinges --------- elasts=[# Element # n2 - end of the element # n1 - beginning of the element # N, Q, M - hinges at the end of the element # N, Q, M - hinges at the beginning of the element 2 1 0 1 0 0; % element 1 3 2 0 0 0 1; % element 2 4 3 0 1 0 0; % element 3 5 4 0 1 0 1; % element 4 6 5 0 0 0 1; % element 5 7 6 0 0 0 0; % element 6 8 7 0 0 0 0]; % element 7 # 1 - hinge 'true' (axial, shear, moment hinges) #

2. Assembling and solving the boundary problem equations (4.5), carried out by the function LaheGerberBeamQM(baasi0,Ntoerkts,esQkoormus,esFjoud,sSolmF,tsolm,tSiire, krdn,selem). The program has numbered the forces at element ends of the frame as shown in Fig. 4.8.
The initial parameter vectors of the elements are given in excerpt 4.4 from the computing diary.

Figure 4.8: Numeration of displacements and forces of the Gerber beam

$\includegraphics[width=1.0\textwidth]{joonised/talaEST323Axnumbr.eps}$

The support reactions of the beam in global coordinates are given in excerpt 4.5 from the computing diary.

Computing diary excerpt 4.4

=============================
Initial parameter vector 
Element No     Q         M 
-----------------------------
   1     -59.000    236.000
   2     -39.000      0.000
   3     -60.000    104.000
   4     -44.000      0.000
   5      34.000      0.000
   6     -56.000     68.000
   7     -20.000     20.000
-----------------------------

Computing diary excerpt 4.5

Support reactions begin from X row: 29  
==========================================
 No         X        Node    Cz <=> 1
                             Cy <=> 2 
------------------------------------------ 
  
 29   -5.900000e+01    1         1 
 30    2.360000e+02    1         2 
 31   -1.250000e+02    3         1 
 32   -9.000000e+01    6         1 
 33   -6.400000e+01    7         1 
------------------------------------------

Testing a static equilibrium for the Gerber beam EST
Consider next a static equilibrium of the beam shown in Figs. 4.7 and 4.8. Let us project the forces onto the Z-axis:

$\displaystyle \Sigma Z = 0; \hfill \quad C_{1}+C_{3}+C_{4}+C_{5}+F_{1}+F_{2}+F_{3}+F_{4}+F_{5}+q\cdot16 = \qquad\qquad\qquad$

$\displaystyle - 59.0 - 125.0 - 90.0 - 64.0 + 20.0 + 40.0 + 30.0 + 100.0 + 20.0 + 8.0\cdot 16 = 0.0$ (4.6)

We now write equation (4.7) of the sum of the moments and the moments of the forces acting about point 1 shown in Figs. 4.7 and 4.8:

$\displaystyle \Sigma M_{1} = 0; \quad C_{2}-12.0\cdot C_{3}-22.0\cdot C_{4}-30.0\cdot C_{5}-4.0\cdot F_{1}-8.0\cdot F_{2}-16.0\cdot F_{3} \quad$

$\displaystyle -26.0\cdot F_{4}-31.0\cdot F_{5}-12.0\cdot 16.0\cdot q = 236.0+12.0\cdot 125.0+22.0\cdot 90.0 \quad$

$\displaystyle +30.0\cdot 64.0-4.0\cdot 20.0 -8.0\cdot 40.0-16.0\cdot 30.0-26.0\cdot 100.0-31.0\cdot 20.0 \quad$

$\displaystyle -12.0\cdot 16.0\cdot 8.0 = 0.0 \quad$ (4.7)

The calculations with equations (4.6) and (4.7) have verified the static equilibrium of the Gerber beam EST.
3. Output: the forces determined by the transfer matrix are shown in excerpt 4.6 from the computing diary.

Computing diary excerpt 4.6 ( spESTGerberBeamQM.m )

#======================================================================= Element forces determined by transfer matrix #======================================================================= Forces of element no 1 of length 4.000 m The element is divided into 4 parts shear force Q - 59.000 59.000 59.000 59.000 59.000 moment force M - -236.000 -177.000 -118.000 -59.000 0.000 ------------------------------------------------------------------- Forces of element no 2 of length 8.000 m The element is divided into 4 parts shear force Q - 39.000 23.000 -33.000 -49.000 -65.000 moment force M - 0.000 62.000 92.000 10.000 -104.000 ------------------------------------------------------------------- Forces of element no 3 of length 2.000 m The element is divided into 4 parts shear force Q - 60.000 56.000 52.000 48.000 44.000 moment force M - -104.000 -75.000 -48.000 -23.000 0.000 ------------------------------------------------------------------- Forces of element no 4 of length 6.000 m The element is divided into 4 parts shear force Q - 44.000 32.000 -10.000 -22.000 -34.000 moment force M - 0.000 57.000 66.000 42.000 0.000 ------------------------------------------------------------------- Forces of element no 5 of length 2.000 m The element is divided into 4 parts shear force Q - -34.000 -34.000 -34.000 -34.000 -34.000 moment force M - 0.000 -17.000 -34.000 -51.000 -68.000 ------------------------------------------------------------------- Forces of element no 6 of length 8.000 m The element is divided into 4 parts shear force Q - 56.000 56.000 -44.000 -44.000 -44.000 moment force M - -68.000 44.000 156.000 68.000 -20.000 ------------------------------------------------------------------- Forces of element no 7 of length 1.000 m The element is divided into 4 parts shear force Q - 20.000 20.000 20.000 20.000 20.000 moment force M - -20.000 -15.000 -10.000 -5.000 0.000 ------------------------------------------------------------------- Forces of element no 4 at x = 1.999999 shear force Q - 28.000 moment force M - 72.000 ------------------------------------- Forces of element no 2 at x = 3.999999 shear force Q - 7.000 moment force M - 92.000 ------------------------------------- Forces of element no 6 at x = 3.999999 shear force Q - 56.000 moment force M - 156.000 -------------------------------------

Figure 4.9: Internal forces diagrams of the Gerber beam EST

$\includegraphics[width=125mm]{joonised/TalaarvutusA_MeM.eps}$
[Bending moment diagram]

$\includegraphics[width=125mm]{joonised/TalaarvutusA_MeQ.eps}$
[Shear force Q diagram]

The bending moment and shear force Q diagrams of the Gerber beam EST are shown in Fig. 4.9.
In Fig. 4.10, the elements, and in Fig. 4.11, the sparsity pattern of matrix spA of the Gerber beam are shown.

The displacements can be computed with the GNU Octave program spESTGerberBeamWFI.m.

Figure 4.10: Elements of the Gerber beam EST

$\includegraphics[width=0.97\textwidth]{joonised/GerberiTala_ESTe.eps}$

Figure 4.11: Sparsity pattern of matrix spA of the Gerber beam EST

$\includegraphics[width=0.78\textwidth]{joonised/GerberiTalaEST_h6reE.eps}$

$\displaystyle \Sigma Z = 0; \hfill \quad C_{1}+C_{3}+C_{4}+C_{5}+F_{1}+F_{2}+F_{3}+F_{4}+F_{5}+q\cdot16 = \qquad\qquad\qquad$
$\displaystyle - 59.0 - 125.0 - 90.0 - 64.0 + 20.0 + 40.0 + 30.0 + 100.0 + 20.0 + 8.0\cdot 16 = 0.0$			(4.6)

$\displaystyle \Sigma M_{1} = 0; \quad C_{2}-12.0\cdot C_{3}-22.0\cdot C_{4}-30.0\cdot C_{5}-4.0\cdot F_{1}-8.0\cdot F_{2}-16.0\cdot F_{3} \quad$
$\displaystyle -26.0\cdot F_{4}-31.0\cdot F_{5}-12.0\cdot 16.0\cdot q = 236.0+12.0\cdot 125.0+22.0\cdot 90.0 \quad$
$\displaystyle +30.0\cdot 64.0-4.0\cdot 20.0 -8.0\cdot 40.0-16.0\cdot 30.0-26.0\cdot 100.0-31.0\cdot 20.0 \quad$
$\displaystyle -12.0\cdot 16.0\cdot 8.0 = 0.0 \quad$			(4.7)