Next: 4.2 Illustrative beam problem Up: 4. Statically determinate problems Previous: 4. Statically determinate problems
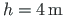 , height of the frame
, height of the frame
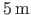 ,
span length
,
span length
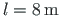 .
The rafter 2-3 is loaded with a vertical uniform load
.
The rafter 2-3 is loaded with a vertical uniform load
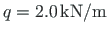 , the
rafter 3-4 is loaded with a vertical concentrated load
, the
rafter 3-4 is loaded with a vertical concentrated load
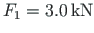 , and
the joint 2 is subjected to a horizontal load
, and
the joint 2 is subjected to a horizontal load
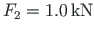 .
.
Consider the load transformation from the global system to the local one shown
in Figs. 4.1 b and 4.2. The force 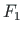 is transformed
to
is transformed
to 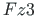 ,
, 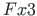 :
:
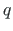 is transformed to
is transformed to 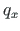 ,
, 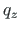 :
:
We wish to compute the reactions and internal forces, and draw the axial force, shear force and bending moment diagrams.
Problem Solving. To solve the problem, we use the EST method. The solving procedure includes the following.
Number_of_frame_nodes=5
Number_of_elements=4
Number_of_support_reactions=4
spNNK=6*Number_of_elements+Number_of_support_reactions;
Number_of_unknowns=spNNK
Forces are calculated on parts ("Nmitmeks") of the element
Nmitmeks=4
Lp=8.0; # graphics axes
# --- Element loads ---
F1=3.0;
L2x=sqrt(4.0^2+1.0^2); # length of
the element
Lpunkt=L2x/2;
F2=1.0;
q=2.0;
sinA2=1.0/L2x;
cosA2=4.0/L2x;
qk=2.0*4.0/L2x;
#esQkoormus qz2 qx2 0.0 L2x
qz2=qk*cosA2; # projection onto z-axis
qx2=-qk*sinA2; # projection onto x-axis
#
#esFjoud Fz3 Fx3 aF3
Fz3=F1*cosA2; # projection onto z-axis
Fx3=F1*sinA2; # projection onto x-axis
aF3=L2x/2;
# ---- load variants -----
load_variant=1
#load_variant=2
#load_variant=3
switch (koormusvariant)
case{1}
disp(' Load variant 1 ')
#Element load in local coordinates # qz qx qA qL # Uniformly distributed load in local coordinate z and x directions LoadsqONelement=4; esQkoormus=zeros(LoadsqONelement,4,ElementideArv);
esQkoormus(1,1:4,1)=[0.0 0.0 0.0 4.0]; esQkoormus(1,1:4,2)=[qz2 qx2 0.0 L2x]; esQkoormus(1,1:4,3)=[0.0 0.0 0.0 L2x]; esQkoormus(1,1:4,4)=[0.0 0.0 0.0 4.0];
# Point load in local coordinate z and x directions kN # Fz, Fx, aF (coordinate of the point of force application) LoadsF_on_Element=5; esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);
esFjoud(1,1:3,1)=[0.0 0.0 0.0]; esFjoud(1,1:3,2)=[0.0 0.0 0.0]; esFjoud(1,1:3,3)=[Fz3 Fx3 aF3]; esFjoud(1,1:3,4)=[0.0 0.0 0.0]; esFjoud(1,1:3,5)=[0.0 0.0 0.0];
#Node forces in global coordinates # sSolmF(forces,1,nodes); forces=[Fx; Fz; My] sSolmF = zeros(3,1,SolmedeArv);
#sSolmF(:,1,1)= 0.0 sSolmF(1,1,2)= F2; #sSolmF(:,1,3)= 0.0 #sSolmF(:,1,4)= 0.0 #sSolmF(:,1,5)= 0.0
#s1F(1,1,1)=0.0; # force Fz #s1F(2,1,1)=0.0; # force Fz #s1F(3,1,1)=0.0; # force My
case{2}
disp(' Load variant 2 ')
case{3}
disp(' Load variant 3 ')
#
otherwise
disp(' No load variant cases ')
endswitch
#==========
# Nodal coordinates
#==========
krdn=[# x z
0.0 0.0; # node 1
0.0 -4.0; # node 2
4.0 -5.0; # node 3
8.0 -4.0; # node 4
8.0 0.0]; # node 5
#==========
# Restrictions on support displacements (on - 1, off - 0)
# Support No u w fi
#==========
tsolm=[1 1 1 0; % node 1
5 1 1 0]; % node 5
#==========
# ------------- Element properties, topology and hinges ---------
elasts=[# Element
# n2 - end of the element
# n1 - beginning of the element
# N, Q, M - hinges at the end of the element
# N, Q, M - hinges at the beginning of the element
2 1 0 0 0 0 0 1; % element 1
3 2 0 0 1 0 0 0; % element 2
4 3 0 0 0 0 0 1; % element 3
5 4 0 0 1 0 0 0]; % element 4
# 1 - hinge 'true' (axial, shear, moment hinges)
#
2. Assembling and solving the boundary problem equations (4.3), carried out by the function LaheFrame3hingeNQM(baasi0,Ntoerkts,esQkoormus,esFjoud,sSolmF,tsolm, tSiire,krdn,selem). The program has numbered the forces at element ends of the frame as shown in Fig. 4.2.
The initial parameter vectors of the elements are given in excerpt 4.1 from the computing diary.
=========================================== Initial parameter vector Element No N Q M ------------------------------------------- 1 6.250 1.600 0.000 2 4.038 -5.433 6.400 3 2.947 1.067 0.000 4 4.750 -2.600 10.400 -------------------------------------------
The support reactions of the frame in global coordinates are shown in excerpt 4.2 from the computing diary.
Support reactions begin from X row: 25
===========================================
No X Node Cx <=> 1
Cz <=> 2
Cy <=> 3
-------------------------------------------
25 +1.600000e+00 1 1
26 -6.250000e+00 1 2
27 -2.600000e+00 5 1
28 -4.750000e+00 5 2
--------------------------------------------
3. Output: the forces determined by the transfer matrix are shown in excerpt 4.3 from the computing diary.
#======================================================================= Element forces determined by transfer matrix #======================================================================= Forces of element no 1 of length 4.000 m The element is divided into 4 parts normal force N - -6.250 -6.250 -6.250 -6.250 -6.250 shear force Q - -1.600 -1.600 -1.600 -1.600 -1.600 moment force M - 0.000 -1.600 -3.200 -4.800 -6.400 ------------------------------------------------------------------------ Forces of element no 2 of length 4.123 m The element is divided into 4 parts normal force N - -4.038 -3.553 -3.068 -2.583 -2.098 shear force Q - 5.433 3.493 1.552 -0.388 -2.328 moment force M - -6.400 -1.800 0.800 1.400 -0.000 ------------------------------------------------------------------------ Forces of element no 3 of length 4.123 m The element is divided into 4 parts normal force N - -2.947 -2.947 -3.674 -3.674 -3.674 shear force Q - -1.067 -1.067 -3.978 -3.978 -3.978 moment force M - 0.000 -1.100 -2.200 -6.300 -10.400 ------------------------------------------------------------------------ Forces of element no 4 of length 4.000 m The element is divided into 4 parts normal force N - -4.750 -4.750 -4.750 -4.750 -4.750 shear force Q - 2.600 2.600 2.600 2.600 2.600 moment force M - -10.400 -7.800 -5.200 -2.600 -0.000 ------------------------------------------------------------------------
Testing a static equilibrium for the frame
Consider next a static equilibrium of the frame shown in Fig. 4.3.
We project the forces onto the X, Z axes and determine the sum of the moments of the forces acting about point 1. The sums of the forces and moments are:
The bending moment M, shear force Q and axial force N diagrams of the statically determined three-hinged frame EST1 are shown in Fig. 4.4.
![\includegraphics[width=73mm]{joonised/raamNa1eMe.eps}](img692xx.png)
[Bending moment diagram] |
|
![\includegraphics[width=69mm]{joonised/raamNa2eQe.eps}](img693xx.png)
[Shear force Q diagram] |
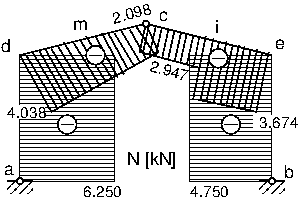
[Axial force N diagram] |
The elements of the frame are depicted in Fig. 4.5 and the sparsity pattern of matrix spA of the frame is shown in Fig. 4.6.
The displacements can be computed with the GNU Octave program spESTframe3hingeLaheWFI.m.