3.3 Illustrative frame problem 3

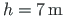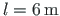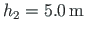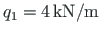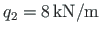Example 3.3 Problem Statement. The frame shown in Fig. 3.15 is of height $h = 7{\,}\mathrm{m}$ and the two spans are of similar length: $l = 6{\,}\mathrm{m}$ . The column 1-2 of length $h_{2} = 5.0{\,}\mathrm{m}$ is loaded with a uniform load $q_{1} = 4{\,}\mathrm{kN/m}$ . The rafter 2-4 is subjected to a vertical uniform load $q_{2} = 8{\,}\mathrm{kN/m}$ . The column 3-4 of length 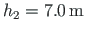$h_{2} = 7.0{\,}\mathrm{m}$ carries a concentrated load 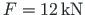$F = 12{\,}\mathrm{kN}$ . 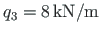The beam 3-5 is loaded with a vertical uniform load $q_{3} = 8{\,}\mathrm{kN/m}$ .

**Figure 3.15:** The frame EST77
$\includegraphics[width=90mm]{joonised/JoumVar7_1.eps}$

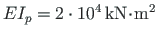Let us suppose that the value of the column flexural rigidity $EI_{p} = 2\cdot 10^{4} {\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}^{2}$ and the rafter flexural rigidity 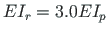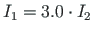$EI_{r} = 3.0EI_{p}$ ( $I_{1} = 3.0\cdot I_{2}$ ); the axial rigidity of the column 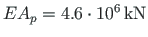$EA_{p} = 4.6\cdot 10^{6}{\,}\mathrm{kN}$ and that of the rafter 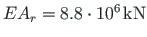$EA_{r} = 8.8\cdot 10^{6}{\,}\mathrm{kN}$ ; the shear rigidity of the column 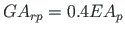$GA_{rp} = 0.4EA_{p}$ and that of the rafter $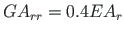GA_{rr} = 0.4EA_{r}$ .

We wish to compute the displacements, reactions, internal forces, and draw the axial force, shear force and bending moment diagrams.

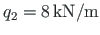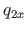Problem Solving. To solve the problem, the EST method is used. Since the element loads are described in local coordinates, we assume the directions of the local coordinates shown in Fig. 3.16. Now let us express the vertical uniform load, $q_{2} = 8{\,}\mathrm{kN/m}$ , in local coordinates ( $q_{2x}$ - projection onto the x-axis, 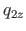$q_{2z}$ - projection onto the z-axis):

$\displaystyle \begin{array}{lll} q_{2k} = q_{2}\cdot 6.0/l_{2}, &\quad where & ... ...{2z} = q_{2k}\cdot\cos\alpha, &\quad where & \cos\alpha = 6.0/l_{2} \end{array}$

(3.10)

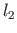Here, $l_{2}$ is the length of the rafter in local coordinates.

As in example 3.1, we carry out the following steps of calculations.

Data input: the number of frame nodes, elements, support reactions; element properties, element loads in local coordinates, node forces in global coordinates, nodal coordinates, topology and hinges, restrictions on support displacements.

$\displaystyle \mathbf{spA}{\cdot}\mathbf{Z} = \mathbf{B}$ (3.11)
Assembling and solving the boundary problem equations (2.1) and (3.11) (prepared and solved by the program). To implement this aim, the program
1. inserts the basic equations of a frame into the equation system,
2. adds the compatibility equations of the displacements at nodes to the equation system,
3. adds the joint equilibrium equations,
4. adds the side conditions (hinges),
5. adds the restrictions on support displacements,
6. solves the compiled system of sparse equations,
7. produces an output: initial parameter vectors for element displacements and forces; support reactions.
Output: element displacements and forces determined by the transfer matrix.

**Figure 3.16:** Numeration of displacements and forces of the frame EST77
$\includegraphics[width=110mm]{joonised/JoumVar7_2.eps}$

1. Input data for the GNU Octave program spESTframe77LaheWFI.m are shown in excerpts from the program: element and nodal loads - excerpt 3.7; nodal coordinates - excerpt 3.8; element properties, topology and hinges - excerpt 3.9.

Program excerpt 3.7 ( spESTframe77LaheWFI.m )

 Number_of_frame_nodes=6 
 Number_of_elements=7
 Number_of_support_reactions=3
 spNNK=12*Number_of_elements+Number_of_support_reactions;
 Number_of_unknowns=spNNK 
 Displacements and forces calculated on parts of the element 'Nmitmeks'.
 Nmitmeks=4
 Lp=12.0; # graphics axis
# --- Element properties ---

  
EIp=20000 # kN/m^2 
EIr=40000 # kN/m^2
# EAp=4.6*10^6 
EAp=4.6*10^15; 
#EAr=6.8*10^6;
EAr=6.8*10^15 
GAp=0.4*EAp;    
GAr=0.4*EAr; 
F3=12;
q1=4.0;
q2=8.0;
q3=8.0;
L2x=sqrt(6.0^2+2.0^2); # length of the element
sinA2=2.0/L2x;
cosA2=6.0/L2x;
qz2v=q2*6.0/L2x;   # load/length of the element
qz1=q1;
qz7=q3;
qz2=qz2v*cosA2;  # projection onto z-axis
qx2=-qz2v*sinA2; # projection onto x-axis

 
baasi0=EIp/5.0  # scaling multiplier for displacements
#baasi0=1.0;

#Element load  in local coordinates 
#  qz     qx     qA      qL 
# Uniformly distributed load in local coordinate z and x directions
LoadsqONelement=4;
esQkoormus=zeros(LoadsqONelement,4,ElementideArv);

esQkoormus(1,1:4,1)=[qz1 0.0 0.0 5.0]; 
esQkoormus(1,1:4,2)=[qz2 qx2 0.0 L2x];
esQkoormus(1,1:4,3)=[0.0 0.0 0.0 7.0];
esQkoormus(1,1:4,4)=[0.0 0.0 0.0 L2x];
esQkoormus(1,1:4,5)=[0.0 0.0 0.0 5.0]; 
esQkoormus(1,1:4,6)=[0.0 0.0 0.0 6.0];
esQkoormus(1,1:4,7)=[qz7 0.0 0.0 6.0];

# # Point load in local coordinate z and x directions kN # Fz, Fx, aF (coordinate of the point of force application) LoadsF_on_Element=5; esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);

esFjoud(1,1:3,1)=[0.0 0.0 0.0];
esFjoud(1,1:3,2)=[0.0 0.0 0.0]; 
esFjoud(1,1:3,3)=[12.0 0.0 4.0]; 
esFjoud(1,1:3,4)=[0.0 0.0 0.0];
esFjoud(1,1:3,5)=[0.0 0.0 0.0];
esFjoud(1,1:3,6)=[0.0 0.0 0.0];
esFjoud(1,1:3,7)=[0.0 0.0 0.0];

# #Node forces in global coordinates # sSolmF(forces,1,nodes); forces=[Fx; Fz; My] sSolmF = zeros(3,1,SolmedeArv);

#sSolmF(:,1,1)= 0.0
#sSolmF(:,1,2)= 0.0
#sSolmF(:,1,3)= 0.0
#sSolmF(:,1,4)= 0.0
#sSolmF(:,1,5)= 0.0
#sSolmF(:,1,6)= 0.0

# #s1F(1,1,1)=0.0; # force Fz #s1F(2,1,1)=0.0; # force Fz #s1F(3,1,1)=0.0; # force My # Support shift - tSiire# # Support shift is multiplied by scaling multiplier tSiire = zeros(3,1,SolmedeArv);

#tSiire(1,1,1)= 0.0
#tSiire(2,1,1)= 0.01*baasi0
#tSiire(2,1,5)= 0.0

**Figure 3.17:** Internal forces diagrams of the frame EST77
$\includegraphics[width=0.97\textwidth]{joonised/JoumVar9_6.eps}$

Program excerpt 3.8 ( spESTframe77LaheWFI.m )
#========== # Nodal coordinates #========== krdn=[# x z 0.0 0.0; # node 1 0.0 -5.0; # node 2 6.0 0.0; # node 3 6.0 -7.0; # node 4 12.0 0.0; # node 5 12.0 -5.0]; # node 6 #========== # #========== # Restrictions on support displacements (on - 1, off - 0) # Support No u w fi #========== tsolm=[1 1 1 0; % node 1 5 0 1 0]; % node 5 #==========

Program excerpt 3.9 ( spESTframe77LaheWFI.m )
# ------------- Element properties, topology and hinges --------- elasts=[# Element properties # n2 - end of the element # n1 - beginning of the element # N, Q, M - hinges at the end of the element # N, Q, M - hinges at the beginning of the element # EIp EAp GAp 2 1 0 0 0 0 0 1; % element 1 EIr EAr GAr 4 2 0 0 0 0 0 0; % element 2 EIp EAp GAp 4 3 0 0 0 0 0 0; % element 3 EIr EAr GAr 6 4 0 0 0 0 0 0; % element 4 EIp EAp GAp 5 6 0 0 1 0 0 0; % element 5 EIr EAr GAr 3 1 0 0 0 0 0 1; % element 6 EIr EAr GAr 5 3 0 0 1 0 0 0]; % element 7 # 1 - hinge 'true' (axial, shear, moment hinges) #

2. Assembling and solving the boundary problem equations (3.11), carried out by the function LaheFrameDFIm(baasi0,Ntoerkts,esQkoormus,esFjoud, sSolmF,tsolm,tSiire, krdn,selem). The program has numbered the displacements and forces of the frame element ends as shown in Fig. 3.16. The unscaled initial parameter vectors of the elements are shown in excerpt 3.7 from the computing diary.

Computing diary excerpt 3.7 ( spESTframe77LaheWFI.m )
-------- Scaling multiplier for displacements = 1/baasi0 -------- ============================================================================ Unscaled initial parameter vector Element u w fi N Q M No ---------------------------------------------------------------------------- 1 -0.000e+00 0.000e+00 -2.842e-03 37.423 -6.458 0.000 2 1.204e-02 4.013e-03 -2.972e-03 24.682 -31.221 17.712 3 -1.021e-02 2.254e-14 -1.220e-03 -12.982 -14.240 37.191 4 1.850e-02 4.598e-03 5.078e-04 18.172 18.775 -62.236 5 2.561e-14 -1.950e-02 8.096e-04 23.558 -11.302 56.510 6 0.000e+00 0.000e+00 -1.943e-03 -25.542 -2.410 0.000 7 2.254e-14 1.021e-02 -1.220e-03 -11.302 -15.392 -51.650 ----------------------------------------------------------------------------

The support reactions of the frame in global coordinates are shown in excerpt 3.8 from the computing diary.

Computing diary excerpt 3.8 ( spESTframe77LaheWFI.m )
Support reactions begin from row X: 85 =========================================== No X Node Cx <=> 1 Cz <=> 2 Cy <=> 3 ------------------------------------------- 85 -3.200000e+01 1 1 86 -3.983333e+01 1 2 87 -5.616667e+01 5 2 --------------------------------------------

3. Output: the element displacements and forces determined by the transfer matrix are shown in excerpt 3.9 from the computing diary. The diagrams of the bending moment M, shear force Q and axial force N of the frame EST77 are shown in Fig. 3.17.
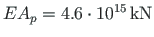Here, the values are determined with the axial stiffness $EA_{p} = 4.6\cdot 10^{15}{\,}\mathrm{kN}$ (with negligible axial deformations, the values coincide with these found with the force method, see [Lah12] ^3.1 Fig. 9.23 on p. 243).

Figure 3.17: Internal forces diagrams of the frame EST77

$\includegraphics[width=0.97\textwidth]{joonised/JoumVar9_6.eps}$

Computing diary excerpt 3.9 ( spESTframe77LaheWFI.m )
#================================================================================= Element displacements and forces determined by transfer matrix #================================================================================= Displacements and forces of element no 1 of length 5.000 m The element is divided into 4 parts displacement u - 0.00000e+00 -1.01694e-14 -2.03388e-14 -3.05082e-14 -4.06777e-14 displacement w - 0.00000e+00 8.48273e-02 1.30835e+00 6.59962e+00 2.08408e+01 rotation fi - -2.84172e-03 -2.63006e-01 -2.08517e+00 -7.03182e+00 -1.66655e+01 normal force N - -37.42345 -37.42345 -37.42345 -37.42345 -37.42345 shear force Q - 6.45764 1.45764 -3.54236 -8.54236 -13.54236 moment force M - 0.00000 4.94705 3.64410 -3.90885 -17.71180 ---------------------------------------------------------------------------- Displacements and forces of element no 2 of length 6.32456 m The element is divided into 4 parts displacement u - 1.20390e-02 1.20390e-02 1.20390e-02 1.20390e-02 1.20390e-02 displacement w - 4.01301e-03 1.33739e-01 2.01215e+00 1.01372e+01 3.20068e+01 rotation fi - -2.97237e-03 -3.19016e-01 -2.53113e+00 -8.53667e+00 -2.02330e+01 normal force N - -24.68175 -20.88701 -17.09228 -13.29755 -9.50281 shear force Q - 31.22053 19.83633 8.45213 -2.93207 -14.31626 moment force M - -17.71180 22.65220 45.01619 49.38019 35.74419 ---------------------------------------------------------------------------- Displacements and forces of element no 3 of length 7.000 m The element is divided into 4 parts displacement u - -1.02109e-02 -1.02109e-02 -1.02109e-02 -1.02109e-02 -1.02109e-02 displacement w - 2.25374e-14 4.34616e-03 1.05712e-02 7.96109e-01 1.08134e+01 rotation fi - -1.21985e-03 -3.38376e-03 -3.36712e-03 -1.87617e+00 -1.07968e+01 normal force N - 12.98177 12.98177 12.98177 12.98177 12.98177 shear force Q - 14.24039 14.24039 14.24039 2.24039 2.24039 moment force M - -37.19081 -12.27013 12.65055 22.57123 26.49192 ---------------------------------------------------------------------------- Displacements and forces of element no 4 of length 6.32456 m The element is divided into 4 parts displacement u - 1.84970e-02 1.84970e-02 1.84970e-02 1.84970e-02 1.84970e-02 displacement w - 4.59761e-03 2.70421e-03 -5.45432e-04 -3.91437e-03 -6.16566e-03 rotation fi - 5.07846e-04 1.75676e-03 2.22336e-03 1.90766e-03 8.09646e-04 normal force N - -18.17178 -18.17178 -18.17178 -18.17178 -18.17178 shear force Q - -18.77538 -18.77538 -18.77538 -18.77538 -18.77538 moment force M - 62.23611 32.54962 2.86313 -26.82336 -56.50985 ---------------------------------------------------------------------------- Displacements and forces of element no 5 of length 5.000 m The element is divided into 4 parts displacement u - 2.56069e-14 1.92051e-14 1.28034e-14 6.40172e-15 -3.15544e-30 displacement w - -1.94975e-02 -1.84861e-02 -1.41636e-02 -7.63366e-03 -3.25087e-14 rotation fi - 8.09646e-04 -2.28074e-03 -4.48815e-03 -5.81260e-03 -6.25409e-03 normal force N - -23.55832 -23.55832 -23.55832 -23.55832 -23.55832 shear force Q - 11.30197 11.30197 11.30197 11.30197 11.30197 moment force M - -56.50985 -42.38239 -28.25493 -14.12746 0.00000 ---------------------------------------------------------------------------- Displacements and forces of element no 6 of length 6.000 m The element is divided into 4 parts displacement u - 0.00000e+00 5.63434e-15 1.12687e-14 1.69030e-14 2.25374e-14 displacement w - 0.00000e+00 2.89162e-03 5.64769e-03 8.13265e-03 1.02109e-02 rotation fi - -1.94281e-03 -1.89763e-03 -1.76207e-03 -1.53614e-03 -1.21985e-03 normal force N - 25.54236 25.54236 25.54236 25.54236 25.54236 shear force Q - 2.40988 2.40988 2.40988 2.40988 2.40988 moment force M - 0.00000 3.61482 7.22964 10.84447 14.45929 ---------------------------------------------------------------------------- Displacements and forces of element no 7 of length 6.000 m The element is divided into 4 parts displacement u - 2.25374e-14 2.50305e-14 2.75235e-14 3.00166e-14 3.25097e-14 displacement w - 1.02109e-02 1.23428e-01 1.80884e+00 9.11559e+00 2.87928e+01 rotation fi - -1.21985e-03 -2.99640e-01 -2.39748e+00 -8.09475e+00 -1.91914e+01 normal force N - 11.30197 11.30197 11.30197 11.30197 11.30197 shear force Q - 15.39165 3.39165 -8.60835 -20.60835 -32.60835 moment force M - 51.65010 65.73758 61.82505 39.91253 0.00000 ----------------------------------------------------------------------------

Forces of element  3  at x = 4.00 m 
 displacement u - -1.02109e-02   
 displacement w -  1.21608e-02   
 rotation    fi - -2.96185e-03   
 normal force N -   12.98177   
 shear force  Q -    2.24039   
 moment force M -   19.77075   
-----------------------------------
Forces of element  3  at x = 3.99 m   
 displacement u - -1.02109e-02   
 displacement w -  1.21608e-02   
 rotation    fi - -2.96185e-03   
 normal force N -   12.98177   
 shear force  Q -   14.24039   
 moment force M -   19.77073   
-----------------------------------

Figure 3.18: Boundary forces of the frame EST77

$\includegraphics[width=1.0\textwidth]{joonised/JoumVar9_7.eps}$

Testing a static equilibrium for the frame
Consider now a static equilibrium of the frame shown in Fig. 3.18 a. We project the forces onto the X and Z axes. The sum of the moments and the moments of the forces acting about point a (shown in Fig. 3.18 a) are:

$\displaystyle \Sigma X$ $\textstyle =$ $\displaystyle 0;\quad -32.0 + 25.541 + 4\cdot 5 - 2.240 - 32.608 = -1.0\cdot 10^{-3} \cong 0$

$\displaystyle \Sigma Y$ $\textstyle =$ $\displaystyle 0;\quad 39.833 - 2.410 - 8\cdot 6 - 12.982 - 32.608 + 56.167 = 7.1\cdot 10^{-15} \cong 0$

$\displaystyle \Sigma M_{a}$ $\textstyle =$ $\displaystyle 0;\quad -4\cdot 5\cdot 2.5 - 8\cdot 6 \cdot 3 - 12.982\cdot 6 + 2.240\cdot 7$

$\textstyle +$ $\displaystyle \left( -32.608 + 56.167\right)\cdot 12 - 26.492 = 4.0\cdot 10^{-3} \cong 0$ (3.12)

Consider next a static equilibrium of the frame shown in Fig. 3.18 b. Let us project the forces onto the X and Z axes. Now, the sum of the moments and the moments of the forces acting about point a (shown in Fig. 3.18 b) are:

$\displaystyle \Sigma X$ $\textstyle =$ $\displaystyle 0;\quad - 25.541 + 12 + 2.240 + 11.302 = -1.0\cdot 10^{-3} \cong 0$

$\displaystyle \Sigma Y$ $\textstyle =$ $\displaystyle 0;\quad + 2.4103 + 12.982 - 8\cdot 6 + 32.608 = -7.1\cdot 10^{-15} \cong 0$

$\displaystyle \Sigma M_{a}$ $\textstyle =$ $\displaystyle 0;\quad - 2.240\cdot 7 + 12.982\cdot 6 + 26.492 -12\cdot 4$

$\textstyle -$ $\displaystyle 8\cdot 6\cdot 9 + 32.608\cdot 12 = -5.68\cdot 10^{-14} \cong 0$ (3.13)

The calculations with Eqs. (3.13) and (3.13) have verified the static equilibrium of the frame.
The elements and the sparsity pattern of matrix spA of the frame EST77 are shown in Figs. 3.19 and 3.20, respectively.

Figure 3.19: Elements of the frame EST77

$\includegraphics[width=0.84\textwidth]{joonised/RaamEST77en.eps}$

Figure 3.20: Sparsity pattern of matrix spA of the frame EST77

$\includegraphics[width=0.75\textwidth]{joonised/RaamEST77_sparse.eps}$

$\displaystyle \Sigma X$	$\textstyle =$	$\displaystyle 0;\quad -32.0 + 25.541 + 4\cdot 5 - 2.240 - 32.608 = -1.0\cdot 10^{-3} \cong 0$
$\displaystyle \Sigma Y$	$\textstyle =$	$\displaystyle 0;\quad 39.833 - 2.410 - 8\cdot 6 - 12.982 - 32.608 + 56.167 = 7.1\cdot 10^{-15} \cong 0$
$\displaystyle \Sigma M_{a}$	$\textstyle =$	$\displaystyle 0;\quad -4\cdot 5\cdot 2.5 - 8\cdot 6 \cdot 3 - 12.982\cdot 6 + 2.240\cdot 7$
	$\textstyle +$	$\displaystyle \left( -32.608 + 56.167\right)\cdot 12 - 26.492 = 4.0\cdot 10^{-3} \cong 0$	(3.12)

$\displaystyle \Sigma X$	$\textstyle =$	$\displaystyle 0;\quad - 25.541 + 12 + 2.240 + 11.302 = -1.0\cdot 10^{-3} \cong 0$
$\displaystyle \Sigma Y$	$\textstyle =$	$\displaystyle 0;\quad + 2.4103 + 12.982 - 8\cdot 6 + 32.608 = -7.1\cdot 10^{-15} \cong 0$
$\displaystyle \Sigma M_{a}$	$\textstyle =$	$\displaystyle 0;\quad - 2.240\cdot 7 + 12.982\cdot 6 + 26.492 -12\cdot 4$
	$\textstyle -$	$\displaystyle 8\cdot 6\cdot 9 + 32.608\cdot 12 = -5.68\cdot 10^{-14} \cong 0$	(3.13)