next up previous contents index
Next: 3.5 Illustrative truss problem Up: 3. Statically indeterminate problems Previous: 3.3 Illustrative frame problem


3.4 Illustrative continuous beam problem

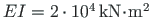Example 3.4   Problem Statement. Given the continuous beam depicted in Fig. 3.21, find the reactions, displacements and internal forces. Draw the shear force and bending moment diagrams. Assume that the value of the beam flexural rigidity $EI = 2\cdot 10^{4} {\,}\mathrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m}^{2}$ and the shear rigidity $GA_{r} = 1.0\cdot 10^{15}{\,}\mathrm{kN}$. 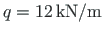The dead loading is a uniform load $q = 12{\,}\mathrm{kN/m}$ (load case 1). The beam is also subjected to a live loading (load cases 2 and 3). 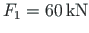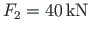The beam is simultaneously loaded with forces $F_{1} = 60{\,}\mathrm{kN}$ and $F_{2} = 40{\,}\mathrm{kN}$ (load case 2). 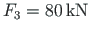In load case 3, it is loaded with force $F_{3} = 80{\,}\mathrm{kN}$.

Figure 3.21: The continuous beam EST
\includegraphics[width=132mm]{joonised/ESTjatkvtala_en.eps}


Problem Solving. To solve the problem, we use the EST method. The solving procedure includes the following.
  1. Data input: the number of beam nodes, elements, support reactions; element properties, element loads in local coordinates, node forces in global coordinates, nodal coordinates, the topology and hinges, restrictions on support displacements.

    $\displaystyle \mathbf{spA}{\cdot}\mathbf{Z} = \mathbf{B}$     (3.14)

  2. Assembling and solving the boundary problem equations (2.1) and (3.14) (prepared and solved by the program). To implement this aim, the program
    1. inserts the basic equations of beam into the equation system,
    2. adds the compatibility equations of the displacements at nodes to the equation system,
    3. adds the joint equilibrium equations,
    4. adds the side conditions (hinges),
    5. adds the restrictions on support displacements,
    6. solves the compiled system of sparse equations,
    7. produces an output: initial parameter vectors for element displacements and forces; support reactions.
  3. Output: element displacements and forces determined by the transfer matrix.

Figure 3.22: Numeration of displacements and forces of the continuous beam EST
\includegraphics[width=140mm]{joonised/ESTjatkvtalaKJS.eps}

1. Input data for the GNU Octave program spESTbeamLaheWFI.m are shown in excerpts from the program: element and nodal loads - excerpt 3.10; nodal coordinates - excerpt 3.11; element properties, topology and hinges - excerpt 3.12.

Program excerpt 3.10 ( spESTbeamLaheWFI.m )   
 Number_of_beam_nodes=5 
 Number_of_elements=4
 Number_of_support_reactions=5
 spNNK=8*Number_of_elements+Number_of_support_reactions;
 Number_of_unknowns=spNNK 
 Displacements and forces calculated on parts of the element 'Nmitmeks'.
 Nmitmeks=5
 Lp=24.0; # graphics axis 
# --- Element properties ---

  
EI=20000 # kN/m^2  
GA=1.0*10^15
F1=60;
F2=40;
F3=80;
qz=12.0;

 
baasi0=EI/8.0  # scaling multiplier for displacements
#baasi0=1.0;

# ---- load variants -----

load_variant=1
#load_variant=2
#load_variant=3
 koormusvariant=load_variant
#koormusvariant=2
#koormusvariant=3

switch (koormusvariant)
case{1}
#
disp(' Load variant 1 ')
#disp(' Element load  in local coordinates ')
# Uniformly distributed load in local coordinate z direction
LoadsqONelement=4;
esQkoormus=zeros(LoadsqONelement,3,ElementideArv);

esQkoormus(1,1:3,1)=[qz 0.0 8.0]; 
esQkoormus(1,1:3,2)=[qz 0.0 8.0];
esQkoormus(1,1:3,3)=[qz 0.0 6.0];
esQkoormus(1,1:3,4)=[qz 0.0 2.0];

# Point load in local coordinate z direction
LoadsF_on_Element=5; 
# 2 - Fz, aFz (coordinate of the point of force Fz application)
esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);

esFjoud(1,1:2,1)=[0.0 8.0];
esFjoud(1,1:2,2)=[0.0 8.0];
esFjoud(2,1:2,2)=[0.0 8.0];
esFjoud(1,1:2,3)=[0.0 6.0];
esFjoud(1,1:2,4)=[0.0 2.0];

#disp(' Node forces in global coordinates ')
#disp(' Node 1 load ')
# sSolmF(forces,1,nodes); forces=[Fz; My]
sSolmF = zeros(2,1,SolmedeArv);

#sSolmF(1,1,1)= 0.0 # force Fz
#sSolmF(2,1,1)= 0.0 # force My
#sSolmF(:,1,2)= 0.0
#sSolmF(:,1,3)= 0.0
#sSolmF(:,1,4)= 0.0
#sSolmF(:,1,5)= 0.0

# Support shift - tSiire#
# Support shift is multiplied by scaling multiplier
tSiire = zeros(2,1,SolmedeArv);

#tSiire(:,1,1)= 0.0
#tSiire(2,1,1)= 0.01*baasi0
#tSiire(:,1,2)= 0.0
#tSiire(:,1,3)= 0.0
#tSiire(:,1,4)= 0.0
#tSiire(:,1,5)= 0.0

case{2}
disp(' Load variant 2 ')
#disp(' Element load  in local coordinates ')
# Uniformly distributed load in local coordinate z direction
LoadsqONelement=4;
esQkoormus=zeros(LoadsqONelement,3,ElementideArv);

esQkoormus(1,1:3,1)=[0.0 0.0 8.0]; 
esQkoormus(1,1:3,2)=[0.0 0.0 8.0];
esQkoormus(1,1:3,3)=[0.0 0.0 6.0];
esQkoormus(1,1:3,4)=[0.0 0.0 2.0];

# Point load in local coordinate z direction
LoadsF_on_Element=5; 
# 2 - Fz, aFz (coordinate of the point of force Fz application)
esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);

esFjoud(1,1:2,1)=[0.0 8.0];
esFjoud(1,1:2,2)=[F1  1.6];
esFjoud(2,1:2,2)=[F2  4.8];
esFjoud(1,1:2,3)=[0.0 6.0];
esFjoud(1,1:2,4)=[0.0 2.0];

#disp(' Node forces in global coordinates ')
#disp(' Node 1 load ')
# sSolmF(forces,1,nodes); forces=[Fz; My]
sSolmF = zeros(2,1,SolmedeArv);

#sSolmF(1,1,1)= 0.0 # force Fz
#sSolmF(2,1,1)= 0.0 # force My
#sSolmF(:,1,2)= 0.0
#sSolmF(:,1,3)= 0.0
#sSolmF(:,1,4)= 0.0
#sSolmF(:,1,5)= 0.0

# Support shift - tSiire#
# Support shift is multiplied by scaling multiplier
tSiire = zeros(2,1,SolmedeArv);

#tSiire(:,1,1)= 0.0
#tSiire(2,1,1)= 0.01*baasi0
#tSiire(:,1,2)= 0.0
#tSiire(:,1,3)= 0.0
#tSiire(:,1,4)= 0.0
#tSiire(:,1,5)= 0.0

case{3}
disp(' Load variant 3 ')
#disp(' Element load  in local coordinates ')
# Uniformly distributed load in local coordinate z direction
LoadsqONelement=4;
esQkoormus=zeros(LoadsqONelement,3,ElementideArv);

esQkoormus(1,1:3,1)=[0.0 0.0 8.0]; 
esQkoormus(1,1:3,2)=[0.0 0.0 8.0];
esQkoormus(1,1:3,3)=[0.0 0.0 6.0];
esQkoormus(1,1:3,4)=[0.0 0.0 2.0];

# Point load in local coordinate z direction
LoadsF_on_Element=5; 
# 2 - Fz, aFz (coordinate of the point of force Fz application)
esFjoud=zeros(LoadsF_on_Element,2,ElementideArv);

esFjoud(1,1:2,1)=[0.0 8.0];
esFjoud(1,1:2,2)=[0.0 8.0];
esFjoud(2,1:2,2)=[0.0 8.0];
esFjoud(1,1:2,3)=[F3  3.6];
esFjoud(1,1:2,4)=[0.0 2.0];

#disp(' Node forces in global coordinates ')
#disp(' Node 1 load ')
# sSolmF(forces,1,nodes); forces=[Fz; My]
sSolmF = zeros(2,1,SolmedeArv);

#sSolmF(1,1,1)= 0.0 # force Fz
#sSolmF(2,1,1)= 0.0 # force My
#sSolmF(:,1,2)= 0.0
#sSolmF(:,1,3)= 0.0
#sSolmF(:,1,4)= 0.0
#sSolmF(:,1,5)= 0.0

# Support shift - tSiire#
# Support shift is multiplied by scaling multiplier
tSiire = zeros(2,1,SolmedeArv);

#tSiire(:,1,1)= 0.0
#tSiire(2,1,1)= 0.01*baasi0
#tSiire(:,1,2)= 0.0
#tSiire(:,1,3)= 0.0
#tSiire(:,1,4)= 0.0
#tSiire(:,1,5)= 0.0

##
otherwise
disp(' No load variant cases ')
endswitch
##

Program excerpt 3.11 ( spESTbeamLaheWFI.m )   
#==========
#     Nodal coordinates
#==========
krdn=[#  x     
        0.0 ; # node 1
        8.0 ; # node 2
       16.0 ; # node 3
       22.0 ; # node 4
       24.0]; # node 5
#========== 
#
#==========
#  Restrictions on support displacements (on - 1, off - 0)
# Support  No   w  fi 
#==========       
tsolm=[1   1 1 ;  # node 1
       2   1 0 ;  # node 2
       3   1 0 ;  # node 3
       4   1 0 ]; # node 4      
#==========

Program excerpt 3.12 ( spESTbeamLaheWFI.m )   
# ------------- Element properties, topology and hinges ---------
elasts=[# Element properties 
#            n2 - end of the element 
#                  n1 - beginning of the element
#                       N, Q, M -  hinges at the end of the element
#                                N, Q, M -  hinges at the beginning of the element 
# 
   EI  GA    2     1    0 0    0 0;    % element 1
   EI  GA    3     2    0 0    0 0;    % element 2
   EI  GA    4     3    0 0    0 0;    % element 3
   EI  GA    5     4    0 0    0 0];   % element 4
# 1 - hinge 'true' (shear, moment hinges)
#

2. Assembling and solving the boundary problem equations (3.14), carried out by the function LaheBeamDFI(baasi0,Ntoerkts,esQkoormus,esFjoud, sSolmF,tsolm,tSiire, krdn,selem). The program has numbered the displacements and forces of the beam element ends as shown in Fig. 3.22. The unscaled initial parameter vectors of the elements are shown in excerpt 3.10 from the computing diary.

Computing diary excerpt 3.10 (load case 1 spESTbeamLaheWFI.m )   
-- Scaling multiplier for displacements = 1/baasi0 ---
============================================================
 Unscaled initial parameter vector 
Element      w          fi             Q          M 
   No
------------------------------------------------------------
   1   +0.000e+00   +0.000e+00      -47.450     62.533
   2   +0.000e+00   -2.933e-04      -49.650     66.933
   3   +0.000e+00   +1.173e-03      -40.956     53.733
   4   +0.000e+00   +3.133e-04      -24.000     24.000
------------------------------------------------------------

The support reactions of the beam in global coordinates are shown in excerpt 3.11 from the computing diary.

Computing diary excerpt 3.11 (load case 1 spESTbeamLaheWFI.m )   
Support reactions begin from row X: 33 
===========================================
 No         X        Node    Cz <=> 1 
                             Cy <=> 2 
------------------------------------------- 
 33   -4.745000e+01    1         1 
 34   +6.253333e+01    1         2 
 35   -9.820000e+01    2         1 
 36   -8.730556e+01    3         1 
 37   -5.504444e+01    4         1 
--------------------------------------------

    

3. Output

Output of load case 1: the element displacements and forces determined by the transfer matrix are shown in excerpt 3.12 from the computing diary.

The shear force Q and the bending moment diagrams of the beam are shown in Fig. 3.23.

Figure 3.23: Internal forces diagrams of the continuous beam (1st loading)
\includegraphics[width=132mm]{joonised/jatkvtala5cESTm.eps}

Testing a static equilibrium for the beam

Consider a static equilibrium of the beam shown in Fig. 3.23. Let us project the forces onto the Z-axis:

$\displaystyle \Sigma Z = 0;\quad$   $\displaystyle 12\cdot 24 - 47.450 - 98.200 - 87.30556 - 55.04444 = 0$ (3.15)

The sum of the moments and the moments of the forces acting about point 1:
$\displaystyle \begin{array}{ll} \Sigma M_{1} = 0; & 62.53333 - 12\cdot 24 + 98.... ...thrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m} \approx 0 \quad \end{array}$     (3.16)

The calculations with equations (3.15) and (3.16) have verified the static equilibrium of the beam.

        
        

Computing diary excerpt 3.12 (load case 1 spESTbeamLaheWFI.m )   
#=================================================================================
 Element displacements and forces determined by transfer matrix 
#================================================================================= 
Displacements and forces of element no 1 of length 8.000 m 
The element is divided into 5 parts 
 displacement w -  0.000e+00  2.546e-03  5.673e-03 5.560e-03 2.321e-03  1.388e-17
 rotation    fi -  0.000e+00 -2.375e-03 -1.135e-03 1.264e-03 2.364e-03 -2.933e-04
 shear force  Q -    47.450    28.250     9.050    -10.150   -29.350   -48.550
 moment force M -   -62.533    -1.973    27.867     26.987    -4.613   -66.933
----------------------------------------------------------------------------
Displacements and forces of element no 2 of length 8.000 m 
The element is divided into 5 parts 
 displacement w -  0.000e+00  3.222e-03  7.137e-03 7.475e-03 3.898e-03 -1.388e-17
 rotation    fi - -2.933e-04 -2.880e-03 -1.569e-03 1.182e-03 2.915e-03  1.173e-03
 shear force  Q -    49.650    30.450     11.250    -7.950   -27.150    -46.350
 moment force M -   -66.933    -2.853     30.507    33.147     5.067    -53.733
----------------------------------------------------------------------------
Displacements and forces of element no 3 of length 6.000 m 
The element is divided into 5 parts 
 displacement w -  0.000e+00 -1.152e-05  1.033e-03 1.461e-03 8.448e-04 6.939e-18
 rotation    fi -  1.173e-03 -7.491e-04 -7.595e-04 1.053e-04 8.085e-04 3.133e-04
 shear force  Q -    40.956    26.556    12.156     -2.244    -16.644   -31.044
 moment force M -   -53.733   -13.227    10.000     15.947      4.613   -24.000
----------------------------------------------------------------------------
Displacements and forces of element no 4 of length 2.000 m 
The element is divided into 5 parts 
 displacement w - 0.000e+00 -4.149e-05  4.117e-05  1.942e-04  3.793e-04  5.733e-04
 rotation    fi - 3.133e-04 -7.707e-05 -3.139e-04 -4.355e-04 -4.803e-04 -4.867e-04
 shear force  Q -   24.000    19.200     14.400     9.600     4.800      0.000
 moment force M -  -24.000   -15.360     -8.640    -3.840    -0.960      0.000
----------------------------------------------------------------------------

Forces of element  1  at x = 4.000 
 displacement w -  6.10667e-03   
 rotation    fi -  7.33333e-05   
 shear force  Q -   -0.55000   
 moment force M -   31.26667   
-----------------------------------
Forces of element  2  at x = 1.599   
 displacement w -  3.22218e-03   
 rotation    fi - -2.88000e-03   
 shear force  Q -   30.45001   
 moment force M -   -2.85336  
-----------------------------------
Forces of element  2  at x = 4.000 
 displacement w -   7.86667e-03   
 rotation    fi - -2.20000e-04   
 shear force  Q -    1.65000   
 moment force M -   35.66667
-----------------------------------
Forces of element  2  at x = 4.800 
 displacement w -  7.47520e-03   
 rotation    fi -  1.18187e-03   
 shear force  Q -   -7.95000   
 moment force M -   33.14667
-----------------------------------
Forces of element  3  at x = 3.600 
 displacement w -  1.46112e-03   
 rotation    fi -  1.05333e-04   
 shear force  Q -   -2.24444   
 moment force M -   15.94667
-----------------------------------

Output of load case 2: the initial parameter vector and support reactions.

Computing diary excerpt 3.13 (load case 2 spESTbeamLaheWFI.m )   
-- Scaling multiplier for displacements = 1/baasi0 ---
============================================================
 Unscaled initial parameter vector 
Element      w          fi             Q          M 
  No
------------------------------------------------------------
   1   +0.000e+00   +0.000e+00       10.752    -28.672
   2   +0.000e+00   -5.734e-03      -65.536     57.344
   3   +0.000e+00   +4.506e-03       -7.509     45.056
   4   +0.000e+00   -2.253e-03        0.000      0.000
------------------------------------------------------------

The support reactions of the beam in global coordinates are shown in excerpt 3.14 from the computing diary.

Computing diary excerpt 3.14 (load case 2 spESTbeamLaheWFI.m )   
Support reactions begin from row X: 33 
===========================================
 No         X        Node    Cz <=> 1 
                             Cy <=> 2 
------------------------------------------- 
 33   +1.075200e+01    1         1 
 34   -2.867200e+01    1         2 
 35   -7.628800e+01    2         1 
 36   -4.197333e+01    3         1 
 37   +7.509333e+00    4         1 
--------------------------------------------

The element displacements and forces determined by the transfer matrix are shown in excerpt 3.15 from the computing diary.

The shear force Q and the bending moment diagrams of the beam are shown in Fig. 3.24.

Figure 3.24: Internal forces diagrams of the continuous beam (2nd loading)
\includegraphics[width=130mm]{joonised/jatkvtala5bESTm.eps}

        

Testing a static equilibrium for the beam

Consider next a static equilibrium of the beam shown in Fig. 3.24. Let us project the forces onto the Z-axis:

$\displaystyle \Sigma Z = 0;\quad$   $\displaystyle \Sigma Z = 60.0 + 40.0 + 10.75 - 76.29 - 41.97 + 7.51 = 0$ (3.17)

The sum of the moments and the moments of the forces acting about point 1:
$\displaystyle \begin{array}{ll} \Sigma M_{1} = 0; & -28.672 - 60\cdot 9.6 -40\c... ...thrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m} \approx 0 \quad \end{array}$     (3.18)

The calculations with equations (3.17) and (3.18) have verified the static equilibrium of the beam.
        

Computing diary excerpt 3.15 (load case 2 spESTbeamLaheWFI.m )   
#=================================================================================
 Element displacements and forces determined by transfer matrix 
#================================================================================= 
Displacements and forces of element no 1 of length 8.000 m 
The element is divided into 5 parts 
 displacement w - 0.000e+00 -1.468e-03 -4.404e-03 -6.606e-03 -5.872e-03 -6.939e-18
 rotation    fi - 0.000e+00  1.606e-03  1.835e-03  6.881e-04 -1.835e-03 -5.734e-03
 shear force  Q - -10.752    -10.752    -10.752    -10.752    -10.752    -10.752
 moment force M -  28.672     11.469     -5.734    -22.938    -40.141    -57.344
----------------------------------------------------------------------------
Displacements and forces of element no 2 of length 8.000 m 
The element is divided into 5 parts 
 displacement w -  0.000e+00  1.061e-02  1.718e-02 1.654e-02 8.916e-03  2.776e-17
 rotation    fi - -5.734e-03 -6.128e-03 -1.972e-03 2.892e-03 5.904e-03  4.506e-03
 shear force  Q -   65.536      5.536     5.536   -34.464    -34.464    -34.464
 moment force M -  -57.344     47.514    56.371    65.229     10.086    -45.056
----------------------------------------------------------------------------
Displacements and forces of element no 3 of length 6.000 m 
The element is divided into 5 parts 
 displacement w - 0.000e+00 -3.893e-03 -5.190e-03 -4.542e-03 -2.595e-03 -6.939e-18
 rotation    fi - 4.506e-03  2.073e-03  1.802e-04 -1.171e-03 -1.982e-03 -2.253e-03
 shear force  Q -    7.509     7.509     7.509      7.509      7.509      7.509
 moment force M -  -45.056   -36.045   -27.034    -18.022     -9.011      0.000
----------------------------------------------------------------------------
Displacements and forces of element no 4 of length 2.000 m 
The element is divided into 5 parts 
 displacement w -  0.000e+00  9.011e-04  1.802e-03  2.703e-03  3.604e-03 4.506e-03
 rotation    fi - -2.253e-03 -2.253e-03 -2.253e-03 -2.253e-03 -2.253e-03 -2.253e-03
 shear force  Q -    0.000      0.000      0.000      0.000      0.000      0.000
 moment force M -    0.000      0.000      0.000      0.000      0.000      0.000
----------------------------------------------------------------------------

Forces of element  1  at x = 4.000 
 displacement w -  -5.73440e-03   
 rotation    fi -   1.43360e-03   
 shear force  Q - -10.75200   
 moment force M - -14.33600
-----------------------------------
Forces of element  2    at x =  1.599  
 displacement w -  1.06081e-02   
 rotation    fi - -6.12762e-03   
 shear force  Q - 65.53600   
 moment force M - 47.51353  
-----------------------------------

Forces of element  2  at x = 4.000 
 displacement w -   1.78347e-02   
 rotation    fi -   3.71200e-04   
 shear force  Q -   5.53600   
 moment force M -  60.80000 
-----------------------------------
Forces of element  2  at x = 4.800 
 displacement w -   1.65413e-02   
 rotation    fi -   2.89178e-03   
 shear force  Q - -34.46400   
 moment force M -  65.22880  
-----------------------------------
Forces of element  3  at x = 3.600 
 displacement w -  -4.54164e-03   
 rotation    fi -  -1.17146e-03   
 shear force  Q -   7.50933   
 moment force M - -18.02240 
-----------------------------------

Output of load case 3: the initial parameter vector and support reactions.

Computing diary excerpt 3.16 (load case 3 spESTbeamLaheWFI.m )   
-- Scaling multiplier for displacements = 1/baasi0 ---
============================================================
 Unscaled initial parameter vector 
Element      w          fi             Q          M 
  No
------------------------------------------------------------
   1   +0.000e+00   +0.000e+00       -2.016      5.376
   2   +0.000e+00   +1.075e-03        6.048    -10.752
   3   +0.000e+00   -4.301e-03      -38.272     37.632
   4   +0.000e+00   +7.334e-03        0.000      0.000
------------------------------------------------------------

Figure 3.25: Internal forces diagrams of the continuous beam (3rd loading)
\includegraphics[width=130mm]{joonised/jatkvtala5aESTm.eps}

The support reactions of the beam in global coordinates are shown in excerpt 3.17 from the computing diary.

Computing diary excerpt 3.17 (load case 3 spESTbeamLaheWFI.m )   
Support reactions begin from row X: 33 
===========================================
 No         X        Node    Cz <=> 1 
                             Cy <=> 2 
------------------------------------------- 
 33   -2.016000e+00    1         1 
 34   +5.376000e+00    1         2 
 35   +8.064000e+00    2         1 
 36   -4.432000e+01    3         1 
 37   -4.172800e+01    4         1 
--------------------------------------------

The element displacements and forces determined by the transfer matrix are shown in excerpt 3.18 from the computing diary.

The shear force Q and the bending moment diagrams of the beam are shown in Fig. 3.25.

Testing a static equilibrium for the beam

Consider now a static equilibrium of the beam shown in Fig. 3.25. Let us project the forces onto the Z-axis:

$\displaystyle \Sigma Z = 0;\quad$   $\displaystyle \Sigma Z = 80 - 2.016 + 8.064 -44.320 -41.728 = 0$ (3.19)

The sum of the moments and the moments of the forces acting about point 1:
$\displaystyle \begin{array}{ll} \Sigma M_{1} = 0; & 5.376 - 80\cdot 19.6 - 8.06... ...thrm{kN}\hspace*{-2pt}\cdot\hspace*{-2pt}\mathrm{m} \approx 0 \quad \end{array}$     (3.20)

The calculations with equations (3.19) and (3.20) have verified the static equilibrium of the beam.

Computing diary excerpt 3.18 (load case 3 spESTbeamLaheWFI.m )   
#=================================================================================
 Element displacements and forces determined by transfer matrix 
#================================================================================= 
Displacements and forces of element no 1 of length 8.000 m 
The element is divided into 5 parts 
 displacement w - 0.000e+00  2.753e-04  8.258e-04  1.239e-03 1.101e-03 -1.735e-18
 rotation    fi - 0.000e+00 -3.011e-04 -3.441e-04 -1.290e-04 3.441e-04  1.075e-03
 shear force  Q -   2.016      2.016      2.016      2.016      2.016      2.016
 moment force M -  -5.376     -2.150      1.075      4.301      7.526     10.752
----------------------------------------------------------------------------
Displacements and forces of element no 2 of length 8.000 m 
The element is divided into 5 parts 
 displacement w - 0.000e+00 -2.202e-03 -4.542e-03 -5.780e-03 -4.679e-03  0.000e+00
 rotation    fi - 1.075e-03  1.548e-03  1.247e-03  1.720e-04 -1.677e-03 -4.301e-03
 shear force  Q -  -6.048     -6.048     -6.048     -6.048     -6.048     -6.048
 moment force M -  10.752      1.075     -8.602    -18.278    -27.955    -37.632
----------------------------------------------------------------------------
Displacements and forces of element no 3 of length 6.000 m 
The element is divided into 5 parts 
 displacement w -  0.000e+00  5.965e-03  1.133e-02 1.280e-02 8.200e-03 -3.469e-18
 rotation    fi - -4.301e-03 -5.181e-03 -3.305e-03 1.326e-03 5.832e-03  7.334e-03
 shear force  Q -  38.272     38.272     38.272     38.272    -41.728    -41.728
 moment force M - -37.632      8.294     54.221    100.147     50.074      0.000
----------------------------------------------------------------------------
Displacements and forces of element no 4 of length 2.000 m 
The element is divided into 5 parts 
 displacement w - 0.000e+00 -2.934e-03 -5.868e-03 -8.801e-03 -1.174e-02 -1.467e-02
 rotation    fi - 7.334e-03  7.334e-03  7.334e-03  7.334e-03  7.334e-03  7.334e-03
 shear force  Q -   0.000      0.000      0.000      0.000      0.000      0.000
 moment force M -   0.000      0.000      0.000      0.000      0.000      0.000
----------------------------------------------------------------------------

Forces of element  1  at x = 4.000 
 displacement w -  1.07520e-03   
 rotation    fi - -2.68800e-04   
 
 shear force  Q -  2.01600   
 moment force M -  2.68800  
-----------------------------------


Forces of element  2  at x =  1.599  
 displacement w - -2.20201e-03   
 rotation    fi -  1.54829e-03   
 shear force  Q - -6.04800   
 moment force M -  1.07521   
-----------------------------------
Forces of element  2  at x = 4.000 
 displacement w -  -5.37600e-03   
 rotation    fi -   8.06400e-04   
 shear force  Q -  -6.04800   
 moment force M - -13.44000 
-----------------------------------
Forces of element  2  at x = 4.800 
 displacement w -  -5.78028e-03   
 rotation    fi -   1.72032e-04   
 shear force  Q -  -6.04800   
 moment force M - -18.27840  
-----------------------------------
Forces of element  3  at x = 3.600 
 displacement w -    1.27955e-02   
 rotation    fi -    1.32557e-03   
 shear force  Q -  -41.72800   
 moment force M - 100.14720  
-----------------------------------

Figure 3.26: The continuous beam minimum-maximum bending moments3.2
\includegraphics[width=0.99\textwidth]{joonised/Suurimad_MtsenV.eps}
=====================================
 Minimum-maximum bending moments
=====================================
 No     x      Mq    Mmax    Min
-------------------------------------

   1   0.00 -62.53 -33.86  -67.91 
   2   0.80 -28.41  -8.34  -32.18 
   3   1.60  -1.97   9.50   -4.12 
   4   2.40  16.79  19.65   16.25 
   5   3.20  27.87  28.94   22.13 
   6   4.00  31.27  33.95   16.93 
   7   4.80  26.99  31.29    4.05 
   8   5.60  15.03  20.94  -16.51 
   9   6.40  -4.61   2.91  -44.75 
  10   7.20 -31.93 -22.79  -80.68 
  11   8.00 -66.93 -56.18 -124.28 
  12   8.80 -31.05 -25.14  -35.97 
  13   9.60  -2.85  45.74   -2.85 
  14  10.40  17.67  69.61   13.90 
  15  11.20  30.51  86.88   21.91 
  16  12.00  35.67  96.47   22.23 
  17  12.80  33.15  98.38   14.87 
  18  13.60  22.95  60.60   -0.17 
  19  14.40   5.07  15.15  -22.89 
  20  15.20 -20.49 -20.49  -70.77 
  21  16.00 -53.73 -53.73 -136.42 
  22  16.60 -31.32 -31.32  -86.54 
  23  17.20 -13.23  -4.93  -49.27 
  24  17.80   0.55  31.80  -30.99 
  25  18.40  10.00  64.22  -17.03 
  26  19.00  15.13  92.32   -7.39 
  27  19.60  15.95 116.09   -2.08 
  28  20.20  12.44  87.55   -1.08 
  29  20.80   4.61  54.69   -4.40 
  30  21.40  -7.53  17.50  -12.04 
  31  22.00 -24.00 -24.00  -24.00 
  32  24.00   0.00   0.00    0.00 
----------------------------------

Figure 3.27: Elements of the continuous beam EST
\includegraphics[width=0.82\textwidth]{joonised/TalaEST_en.eps}


Figure 3.28: Sparsity pattern of matrix spA of the continuous beam EST
\includegraphics[width=0.75\textwidth]{joonised/TalaEST_sparse.eps}


next up previous contents index
Next: 3.5 Illustrative truss problem Up: 3. Statically indeterminate problems Previous: 3.3 Illustrative frame problem
andres
2014-09-09