3.5 Illustrative truss problem

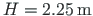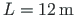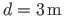Example 3.5 Problem Statement. Given the truss of Fig. 3.29, find the reactions, displacements and internal forces. The height of the truss $H = 2.25{\,}\mathrm{m}$ and the span length $L = 12{\,}\mathrm{m}$ . The panel length $d = 3{\,}\mathrm{m}$ . The dead load reacts on the upper side nodes.

**Figure 3.29:** The truss EST
$\includegraphics[width=120mm]{./joonised/trussESTPy.eps}$

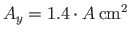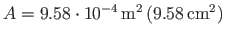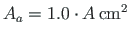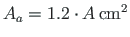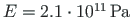Let us assume that the cross-sectional area of the upper side members $A_{y}=1.4\cdot A{\,}\mathrm{cm^{2}}$ where $A=9.58\cdot 10^{-4}{\,}\mathrm{m^{2}} \left( 9.58{\,}\mathrm{cm^{2}}\right)$ , the cross-sectional area of the bottom side members $A_{a}=1.0\cdot A{\,}\mathrm{cm^{2}}$ and that of the diagonal members $A_{a}=1.2\cdot A{\,}\mathrm{cm^{2}}$ . The modulus of elasticity $E=2.1\cdot 10^{11}{\,}\mathrm{Pa}$ .

Problem Statement. To solve the problem, we use the EST method. The solving procedure includes the following.

Data input: the number of truss nodes, elements, support reactions; element properties, node forces in global coordinates, restrictions on support displacements.

$\displaystyle \mathbf{spA}{\cdot}\mathbf{Z} = \mathbf{B}$ (3.21)
Assembling and solving the boundary problem equations (2.1) and (3.21), carried out by the function LaheTrussDFI.m. To implement this aim, the program
1. inserts the basic equations of truss into the equation system,
2. adds the compatibility equations of the displacements at nodes to the equation system,
3. adds the joint equilibrium equations,
4. adds the restrictions on support displacements,
5. solves the compiled system of sparse equations,
6. produces an output: initial parameter vectors for element displacements and forces; support reactions.
Output: the displacements and forces of truss members.

**Figure 3.30:** A free-body diagram of the truss with joint numbers
$\includegraphics[width=0.82\textwidth]{./joonised/trussESTPysolm.eps}$

1. Input data for the GNU Octave program spESTtrussLaheWFI.m are shown in excerpts from the program: element and nodal loads - excerpt 3.13; nodal coordinates - excerpt 3.14; element properties, topology and hinges - excerpt 3.15.

Program excerpt 3.13 ( spESTtrussLaheWFI.m )

 Number_of_truss_nodes=10 
 Number_of_elements=17
 Number_of_support_reactions=4
 d=3.0;  # panel length
 Npanel=4; # panel number
 L=12.0;  # truss span
 H=2.25;  # truss height
 spNNK=8*Number_of_elements+Number_of_support_reactions;
 Number_of_unknowns=spNNK 
 Lp=12.0; # graphics axis 
# --- Element properties ---

  
E=2.1E+11 # Pa 
A=9.58E-04  #  A=9.58 cm2
EAa=Aa*E;
EAy=Ay*E;
EAd=Ad*E;

baasi0=EAy/d # scaling multiplier for displacements
#disp(' Node forces in global coordinates ') # sSolmF(forces,1,nodes); forces=[Fx; Fz] sSolmF = zeros(2,1,SolmedeArv);

sSolmF = zeros(2,1,SolmedeArv);
#sSolmF(:,1,1)=0.0
sSolmF(2,1,2)=Fz/2;  # s2F(2,1)=F/2;
#sSolmF(:,1,3)=0.0
sSolmF(2,1,4)=Fz;    # s4F(2,1)=F;
#sSolmF(:,1,5)=0.0
sSolmF(2,1,6)=Fz;    # s6F(2,1)=F;
#sSolmF(:,1,7)=0.0
sSolmF(2,1,8)= Fz;   # s8F(2,1)=F;
#sSolmF(:,1,9)=0.0
sSolmF(2,1,10)=Fz/2; # s10F(2,1)=F/2;

# Support shift - tSiire# # Support shift is multiplied by scaling multiplier tSiire = zeros(2,1,SolmedeArv);

#tSiire(1,1,1)= 0.0
#tSiire(2,1,1)= 0.01*baasi0
#tSiire(1,1,9)= 0.0
#tSiire(2,1,9)= 0.0

Program excerpt 3.14 ( spESTtrussLaheWFI.m )
#========== # Nodal coordinates #==========

krdn=[#	 x       z
        0.0      0.0  ;   % node 1
        0.0     -2.25 ;   % node 2
        3.0     -0.75 ;   % node 3
        3.0     -2.25 ;   % node 4
        6.0     -1.5  ;   % node 5
        
        6.0     -2.25 ;   % node 6
        9.0     -0.75 ;   % node 7
        9.0     -2.25 ;   % node 8
       12.0      0.0  ;   % node 9
       12.0     -2.25];   % node 10

#========== # #========== # Restrictions on support displacements (on - 1, off - 0) # Support No u w fi #========== tsolm=[1 1 1 0; % node 1 9 1 1 0]; % node 9 #==========

Program excerpt 3.15 ( spESTtrussLaheWFI.m )
# ------------- Element properties, topology --------- elasts=[# Element properties # n2 - end of the element # n1 - beginning of the element # A E;

          2   1  Ad  E;  % element 1
          3   1  Aa  E;  % element 2
          3   2  Ad  E;  % element 3
          4   2  Ay  E;  % element 4
          4   3  Ad  E;  % element 5
          6   4  Ay  E;  % element 6
          5   4  Ad  E;  % element 7
          5   3  Aa  E;  % element 8
          6   5  Ad  E;  % element 9
          8   6  Ay  E;  % element 10
          8   5  Ad  E;  % element 11
          7   5  Aa  E;  % element 12
          8   7  Ad  E;  % element 13
         10   8  Ay  E;  % element 14
         10   7  Ad  E;  % element 15
          9   7  Aa  E;  % element 16
         10   9  Ad  E]; % element 17

2. Assembling and solving the boundary problem equations (3.21), carried out by the function LaheTrussDFI(baasi0,Ntoerkts,esQkoormus,esFjoud,sSolmF,tsolm,tSiire, krdn,selem).The program has numbered the displacements and forces of the truss element ends as shown in Fig. 3.31. The unscaled initial parameter vectors of the elements are shown in excerpt 3.19 from the computing diary.

Figure 3.31: Numeration of displacements and forces of the truss EST

$\includegraphics[width=0.88\textwidth]{./joonised/trussESTPynumb.eps}$

Computing diary excerpt 3.19 (load case 1 spESTtrussLaheWFI.m )
-- Scaling multiplier for displacements = 1/baasi0 --- ============================================================= Unscaled initial parameter vector (Sign Convention 2) Element u w fi N No -------------------------------------------------------------- 1 0.000e+00 -0.000e+00 -2.056e-04 15142.038 2 0.000e+00 0.000e+00 -5.898e-04 36522.315 3 4.768e-04 -8.061e-05 -5.458e-04 -20442.218 4 4.625e-04 1.411e-04 -6.166e-04 18284.075 5 -1.906e-03 -1.022e-04 -2.467e-04 13713.056 6 2.677e-04 1.991e-03 -4.938e-04 25136.301 7 7.426e-04 1.866e-03 -4.740e-04 -7063.113 8 -5.614e-04 1.824e-03 -4.878e-04 17675.521 9 -3.435e-03 -2.132e-21 -1.083e-19 12000.000 10 7.911e-20 3.472e-03 4.938e-04 25136.301 11 -8.331e-04 3.332e-03 4.740e-04 -7063.113 12 8.331e-04 3.332e-03 4.878e-04 17675.521 13 -1.906e-03 1.022e-04 2.467e-04 13713.056 14 -2.677e-04 1.991e-03 6.166e-04 18284.075 15 -7.608e-04 1.750e-03 5.458e-04 -20442.218 16 5.614e-04 1.824e-03 5.898e-04 36522.315 17 -0.000e+00 0.000e+00 2.056e-04 15142.038 ---------------------------------------------------------------

The support reactions of the truss in global coordinates are shown in excerpt 3.20 from the computing diary.

Computing diary excerpt 3.20 (load case 1 spESTtrussLaheWFI.m )
Support reactions begin from row X: 33 =========================================== No X Node Cx <=> 1 Cz <=> 2 ------------------------------------------- 137 +3.543185e+04 1 1 138 -2.400000e+04 1 2 139 -3.543185e+04 9 1 140 -2.400000e+04 9 2 --------------------------------------------

3. Output
Results of computation. The values of displacements and forces of the truss members are presented in Table 3.1.
The verifiable results have been obtained with the finite element method ^3.4 (FEM). The displacements determined by the EST method are 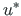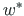$u^{\ast}$ , $w^{\ast}$ (in local coordinates), these determined by the FEM are 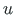, 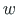(in global coordinates). The displacements 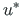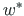$u^{\ast}$ , $w^{\ast}$ of members 1, 5, 9, 13, and 17 compared with the displacements 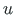, 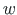of nodes 1, 2, 3, .., 10 are shown in Table 3.1.
The forces and displacements determined by the EST method are of the same value as these determined by the FEM.

Figure 3.32: Support reactions of the truss EST

$\includegraphics[width=0.82\textwidth]{./joonised/trussESTPyToed.eps}$

Testing a static equilibrium for the truss
Consider next a static equilibrium of the truss shown in Fig. 3.32. Let us project the forces onto the X-axis,

$\displaystyle \begin{array}{ccl} \Sigma X = 0; & & 35.43 - 35.43 = 0 \end{array}\vspace*{-8pt}$ (3.22)

and onto the Z-axis,

$\displaystyle \begin{array}{ccl} \Sigma Z = 0; & & 4\cdot 12.0 - 2\cdot 24.0 = 0 \end{array}$ (3.23)

Now we consider the left part of the truss (members 4, 5, 8 are cut through with the cut I-I) shown in Fig. 3.32. Here, the sum of the moments of the forces acting about point 8 is

$\displaystyle \begin{array}{ll} \Sigma M_{1} = 0; & \left(- 24.0 + 6.0 \right)9.0 + 13.713\cdot 6.0 + 35.432\cdot 2.25 = 0 \end{array}$ (3.24)

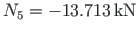where the internal force $N_{5} = -13.713{\,}\mathrm{kN}$ .
The calculations with equations (3.22), (3.23), and (3.24) have verified the static equilibrium of the truss.

Table 3.1: Comparison of the internal forces of the truss
Member EST method (Sign Convention 1) FEM (global coordinates)

No u* w* N u w N

${\,}{\,}{\,}{\,}$ [m] [m] [N] [m] [m] [kN]

1 begin. 0.000e+00 0.000e+00 -15142.038 0.000e+00 0.000e+00

1 end -1.411e-04 4.625e-04 -15142.038 4.625e-02 1.411e-02 -15.1420

2 begin. -0.000e+00 -0.000e+00 -36522.315

2 end -5.614e-04 1.824e-03 -36522.315 -36.5223

3 begin. 4.768e-04 -8.061e-05 20442.218

3 end 7.608e-04 1.750e-03 20442.218 20.4422

4 begin. 4.625e-04 1.411e-04 -18284.075

4 end 2.677e-04 1.991e-03 -18284.075 -18.2841

5 begin. -1.906e-03 -1.022e-04 -13713.056 -1.022e-02 1.906e-01

5 end -1.991e-03 2.677e-04 -13713.056 2.677e-02 1.991e-01 -13.7131

6 begin. 2.677e-04 1.991e-03 -25136.301

6 end 3.056e-20 3.472e-03 -25136.301 -25.1363

7 begin. 7.426e-04 1.866e-03 7063.113

7 end 8.331e-04 3.332e-03 7063.113 7.0631

8 begin. -5.614e-04 1.824e-03 -17675.521

8 end -8.331e-04 3.332e-03 -17675.521 -17.6755

9 begin. -3.435e-03 1.540e-21 -12000.000 -1.133e-16 3.435e-01

9 end -3.472e-03 3.056e-20 -12000.000 -1.196e-16 3.472e-01 -12.0000

10 begin. 3.056e-20 3.472e-03 -25136.301

10 end -2.677e-04 1.991e-03 -25136.301 -25.1363

11 begin. -8.331e-04 3.332e-03 7063.113

11 end -7.426e-04 1.866e-03 7063.113 7.0631

12 begin. 8.331e-04 3.332e-03 -17675.521

12 end 5.614e-04 1.824e-03 -17675.521 -17.6755

13 begin. -1.906e-03 1.022e-04 -13713.056 1.022e-02 1.906e-01

13 end -1.991e-03 -2.677e-04 -13713.056 -2.677e-02 1.991e-01 -13.7131

14 begin. -2.677e-04 1.991e-03 -18284.075

14 end -4.625e-04 1.411e-04 -18284.075 -18.2841

15 begin. -7.608e-04 1.750e-03 20442.218

15 end -4.768e-04 -8.061e-05 20442.218 20.4422

16 begin. 5.614e-04 1.824e-03 -36522.315

16 end 0.000e+00 0.000e+00 -36522.315 -36.5223

17 begin. 0.000e+00 0.000e+00 -15142.038 0.000e+00 0.000e+00

17 end -1.411e-04 -4.625e-04 -15142.038 -4.625e-02 1.411e-02 -15.1420

Figure 3.33: Elements of the truss EST

$\includegraphics[width=0.82\textwidth]{joonised/spESTtruss.eps}$

Figure 3.34: Sparsity pattern of matrix spA of the truss

$\includegraphics[width=0.75\textwidth]{joonised/spESTtruss_sparse_matrix.eps}$

Member	EST method (Sign Convention 1)			FEM (global coordinates)
No	u*	w*	N	u	w	N
${\,}{\,}{\,}{\,}$	[m]	[m]	[N]	[m]	[m]	[kN]
1 begin.	0.000e+00	0.000e+00	-15142.038	0.000e+00	0.000e+00
1 end	-1.411e-04	4.625e-04	-15142.038	4.625e-02	1.411e-02	-15.1420
2 begin.	-0.000e+00	-0.000e+00	-36522.315
2 end	-5.614e-04	1.824e-03	-36522.315			-36.5223
3 begin.	4.768e-04	-8.061e-05	20442.218
3 end	7.608e-04	1.750e-03	20442.218			20.4422
4 begin.	4.625e-04	1.411e-04	-18284.075
4 end	2.677e-04	1.991e-03	-18284.075			-18.2841
5 begin.	-1.906e-03	-1.022e-04	-13713.056	-1.022e-02	1.906e-01
5 end	-1.991e-03	2.677e-04	-13713.056	2.677e-02	1.991e-01	-13.7131
6 begin.	2.677e-04	1.991e-03	-25136.301
6 end	3.056e-20	3.472e-03	-25136.301			-25.1363
7 begin.	7.426e-04	1.866e-03	7063.113
7 end	8.331e-04	3.332e-03	7063.113			7.0631
8 begin.	-5.614e-04	1.824e-03	-17675.521
8 end	-8.331e-04	3.332e-03	-17675.521			-17.6755
9 begin.	-3.435e-03	1.540e-21	-12000.000	-1.133e-16	3.435e-01
9 end	-3.472e-03	3.056e-20	-12000.000	-1.196e-16	3.472e-01	-12.0000
10 begin.	3.056e-20	3.472e-03	-25136.301
10 end	-2.677e-04	1.991e-03	-25136.301			-25.1363
11 begin.	-8.331e-04	3.332e-03	7063.113
11 end	-7.426e-04	1.866e-03	7063.113			7.0631
12 begin.	8.331e-04	3.332e-03	-17675.521
12 end	5.614e-04	1.824e-03	-17675.521			-17.6755
13 begin.	-1.906e-03	1.022e-04	-13713.056	1.022e-02	1.906e-01
13 end	-1.991e-03	-2.677e-04	-13713.056	-2.677e-02	1.991e-01	-13.7131
14 begin.	-2.677e-04	1.991e-03	-18284.075
14 end	-4.625e-04	1.411e-04	-18284.075			-18.2841
15 begin.	-7.608e-04	1.750e-03	20442.218
15 end	-4.768e-04	-8.061e-05	20442.218			20.4422
16 begin.	5.614e-04	1.824e-03	-36522.315
16 end	0.000e+00	0.000e+00	-36522.315			-36.5223
17 begin.	0.000e+00	0.000e+00	-15142.038	0.000e+00	0.000e+00
17 end	-1.411e-04	-4.625e-04	-15142.038	-4.625e-02	1.411e-02	-15.1420