Next: D. Computer programs for Up: C. Transfer matrices Previous: C.1 Transfer matrices of
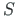 - axial force,
- axial force,
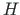 - transverse shear force, see Fig. 5.1.
- transverse shear force, see Fig. 5.1.
Numerical difficulties may occur when the transfer matrix manipulation involves
differences of large numbers (forces and displacements can differ ca 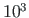 times), leading to inaccuracies in computations [PW94], [PL63]. Round-off errors can be reduced by scaling.
We will scale (multiply) the displacements and rotations by
times), leading to inaccuracies in computations [PW94], [PL63]. Round-off errors can be reduced by scaling.
We will scale (multiply) the displacements and rotations by
 (the scaling multiplier for the displacements).
After solving a system of linear equations of a boundary value problem, we divide
each of the displacements and rotations found by
(the scaling multiplier for the displacements).
After solving a system of linear equations of a boundary value problem, we divide
each of the displacements and rotations found by
 . Displacements and forces at the beginning of members determine
unscaled initial parameter vectors for the structure members.
. Displacements and forces at the beginning of members determine
unscaled initial parameter vectors for the structure members.
The transfer matrix 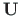 from Eqs. (C.7), (C.9), and (C.10) of a second-order analysis for a frame (Sign Convention 2) can be computed using the GNU Octave function ylfmhvII.m
(p.
from Eqs. (C.7), (C.9), and (C.10) of a second-order analysis for a frame (Sign Convention 2) can be computed using the GNU Octave function ylfmhvII.m
(p. ![]() ).
).
The transfer matrix 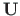 for a frame in compression, Sign Convention 2:
for a frame in compression, Sign Convention 2:
The transfer matrix 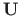 for a frame in tension, Sign Convention 2:
for a frame in tension, Sign Convention 2:
In the case of a uniformly distributed load 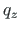 , the loading vector
, the loading vector
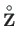 (see Eq. (C.7)) of a second-order analysis
for a frame member under axial compression
(see Eq. (C.7)) of a second-order analysis
for a frame member under axial compression 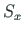 is
is
and for a frame member under axial tension  ,
,
The loading vectors in Tables C.3, C.4, C.5, and C.6 are comparable with those in [Krä91b] and [Bor79b].
The loading vectors of Eqs. (C.11) and (C.12) can be computed using the GNU Octave function ylqvII.m .
In the case of a point load 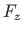 , the loading vector
, the loading vector
 (see Eq. (C.7)) of a second-order analysis
for a frame member under axial compression
(see Eq. (C.7)) of a second-order analysis
for a frame member under axial compression 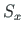 is
is
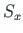 ,
,
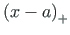 is the Heaviside function:
is the Heaviside function:
The basic system of equations or the frame element of Eq. (C.7) can be rewritten in the form
 can be computed using the GNU Octave function ysplvfmhvII.m
,
in which the GNU Octave function ysplfmhvII.m
(p.
can be computed using the GNU Octave function ysplvfmhvII.m
,
in which the GNU Octave function ysplfmhvII.m
(p.
The loading vectors of a uniformly distributed load and a point load for
a frame can be computed using the GNU Octave functions ylqvII.m
(p. ![]() ) and ylfhvzII.m
(p.
) and ylfhvzII.m
(p. ![]() ).
These functions differentiate between pressure and tensile axial loading.
).
These functions differentiate between pressure and tensile axial loading.
The transfer equations with normal and shear forces (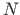 - normal force,
- normal force, 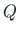 - shear force shown in Fig. 5.1):
- shear force shown in Fig. 5.1):
and the
transfer matrix
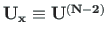 for a compressive normal force (Sign Conven-tion 2)
for a compressive normal force (Sign Conven-tion 2)
while
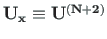 for a tensile normal force (Sign Convention 2)
for a tensile normal force (Sign Convention 2)