A.1.1 Introduction to sparse matrices

Figure A.1: Sparsity pattern of matrix spA

For calculating support reactions and interaction forces on statically determinate hinged beams, also known as Gerber ^A.5 A.6 beams (see Fig. A.2), we have a system of equilibrium equations where the coefficient matrix is sparse. The sparsity pattern of this matrix spA is shown in Fig. A.1.

Figure A.2: Assembly sequence of a Gerber beam

To prevent a large number of calculations, this system is decomposed in such a way that an unknown force could be calculated directly with each equilibrium equation.

Consider the equilibrium equations for the beams in Fig. A.2:
beam 6-8

$$\Sigma M_{6} = 0; \qquad \;\;\; X_{8}\cdot 6 + F_{3}\cdot 2 + q\cdot 6\cdot 3 = 0$$ (A.1)

$$\Sigma M_{8} = 0; -X_{7}\cdot 6 + F_{3}\cdot 4 + q\cdot 6\cdot 3 = 0$$ (A.2)

beam 8-12

$$\Sigma M_{11} = 0; -X_{8}\cdot 10 - X_{4}\cdot 8 + F_{4}\cdot 4 - F_{5}\cdot 1 = 0$$ (A.3)

$$\Sigma M_{9} = 0; -X_{8}\cdot 2 + X_{5}\cdot 8 - F_{4}\cdot 4 - F_{5}\cdot 9 = 0$$ (A.4)

beam 3-6

$$\Sigma M_{3} = 0; -X_{7}\cdot 10 + X_{3}\cdot 8 - F_{2}\cdot 4 - q\cdot 10\cdot 5 = 0$$ (A.5)

$$\Sigma M_{5} = 0; -X_{7}\cdot 2 - X_{6}\cdot 8 + F_{2}\cdot 4 + q\cdot 10\cdot \left( 5 -2\right) = 0$$ (A.6)

beam 1-3

$$\Sigma Z = 0; X_{6}- X_{2} + F_{1} = 0$$ (A.7)

$$\Sigma M_{1} = 0; X_{1} + X_{6}\cdot 4 + F_{1}\cdot 4 = 0$$ (A.8)

Now rewrite the systems of equations (A.1)-(A.8) in matrix form:

$$\left. \begin{array}{l} 1.\:\: \Sigma M_{6} = 0; \\ 2.\:\: \Sigm... ... X_{3} \\ X_{4} \\ X_{5} \\ X_{6} \\ X_{7} \\ X_{8} \end{array} \right] =$$

$$% = -\left[ \begin{array}{c} F_{3}\cdot 2 + q\cdot 6\cdot 3 \\ F... ...0\cdot \left( 5 -2\right) \\ F_{1} \\ F_{1}\cdot 4 \end{array} \right] \qquad$$ (A.9)

We have obtained the sparse system (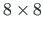$8\times 8$) of equilibrium equations

$$\mathbf{A}\cdot\mathbf{X} = -\mathbf{B}$$ (A.10)

where

$$\mathbf{A}= \left[ \begin{array}{rrrrrrrr} 0 & 0 & 0 & 0 & 0 & 0 ... ...264 \\ -380 \\ 580 \\ 560 \\ -400 \\ -20 \\ -80 \end{array} \right] \quad$$ (A.11)

The Gerber beam support reactions are calculated by hand in the reverse order to that of the assembly sequence (see calculating order in Eqs. (A.1)-(A.9), and Fig. A.2). The sparsity pattern of the matrix 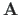$\mathbf{A}$ of Eq. (A.11) is shown in Fig. A.1.

The non-zero elements of the matrix can be represented as the row (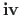$\mathbf{iv}$), column (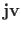$\mathbf{jv}$) and data (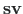$\mathbf{sv}$) vectors in Eq. (A.12).

$$\mathbf{iv} \left[ 1{\;}{\;}{\;}{\;}{\;} 2{\;}{\;}{\;}{\;}{\;}{\;}{\;} 3{\;}{... ...}{\;}{\;}{\;} 6{\;}{\;}{\;}{\;}{\;}{\;} 7{\;}{\;} 7{\;}{\;} 8{\;}{\;} 8 \right]$$

$$\mathbf{jv} \left[ 8{\;}{\;}{\;}{\;}{\;} 7{\;}{\;}{\;}{\;}{\;}{\;}{\;} 4{\;}{... ...}{\;}{\;}{\;} 7{\;}{\;}{\;}{\;}{\;}{\;} 2{\;}{\;} 6{\;}{\;} 1{\;}{\;} 6 \right]$$ (A.12)

$$\mathbf{sv} \left[ 6{\;}{\;} -6{\;}{\;} -8{\;}{\;} -10{\;}{\;} 8{\;}{\;} -2{\... ...10{\;}{\;} -8{\;}{\;} -2{\;}{\;} -1{\;}{\;} 1{\;}{\;} 1{\;}{\;} 4 \right] \quad$$