Next: 5.3.3 The particular solution Up: 5.3 Solutions of a Previous: 5.3.1 The set of
Differentiating the solution
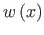 of Eq. (5.46) to a homogeneous differential equation for the compressive axial force (Sign Convention 1)
of Eq. (5.46) to a homogeneous differential equation for the compressive axial force (Sign Convention 1)
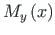 :
:
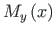 , we obtain the shear force
, we obtain the shear force
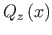 :
:
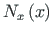 and axial displacement
and axial displacement
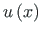 we take (Sign Convention 1)
we take (Sign Convention 1)
These equations can now be written in matrix form:
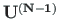 is the transfer matrix for the compressive axial force (Sign Convention 1).
is the transfer matrix for the compressive axial force (Sign Convention 1).
For the tensile axial force (Sign Convention 1), the transfer equations are given by
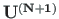 is the transfer matrix:
is the transfer matrix:
For the compressive axial force (Sign Convention 2), the transfer equations are given by
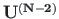 is the transfer matrix:
is the transfer matrix:
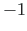 (see Sign Convention, Fig. 1.2).
(see Sign Convention, Fig. 1.2).
For the tensile axial force (Sign Convention 2), the transfer equations are given by
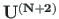 is the transfer matrix:
is the transfer matrix:
The transformation matrices of Eqs. (5.62) and (5.64) can be represented
with the GNU Octave function ylfmII.m
(p. ![]() ).
).