Järgmine: E.2 Programmid murtud tala Üles: E. Arvutiprogrammid Eelmine: E. Arvutiprogrammid
 ja momendid
ja momendid  ,
,
 ,
,
 ning
ning 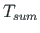 lausmomendiga
lausmomendiga 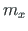 koormatud konsoolis.
koormatud konsoolis.
Kasutab funktsioone
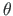 ja momendid
ja momendid 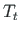 ,
,
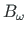 ,
,
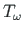 ning
ning 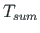 koondmomendiga
koondmomendiga 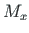
Kasutab funktsioone
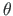 ja momendid
ja momendid 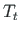 ,
,
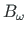 ,
,
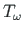 ning
ning 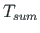 bimomendiga
bimomendiga
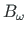 koormatud konsoolis.
koormatud konsoolis.
Kasutab funktsioone
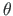 ja momendid
ja momendid 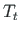 ,
,
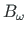 ,
,
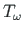 ning
ning 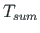 lausmomendiga
lausmomendiga 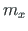 koormatud talas.
koormatud talas.
Kasutab funktsioone
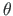 ja momendid
ja momendid 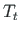 ,
,
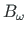 ,
,
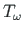 ning
ning 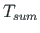 koondmomendiga
koondmomendiga 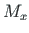 koormatud talas.
koormatud talas.
Kasutab funktsioone
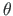 ja momendid
ja momendid 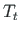 ,
,
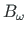 ,
,
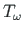 ning
ning 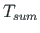 bimomendiga
bimomendiga
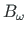 koormatud talas.
koormatud talas.
Kasutab funktsioone
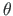 ja momendid
ja momendid 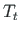 ,
,
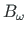 ,
,
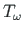 ning
ning 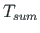 pikijõuga
pikijõuga 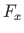 koormatud talas.
koormatud talas.
Kasutab funktsioone
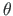 ja momendid
ja momendid 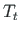 ,
,
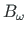 ,
,
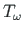 ning
ning 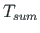 laus- ja koondkoormusega
laus- ja koondkoormusega 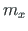 ,
, 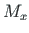 ning bimomendiga
ning bimomendiga
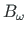 koormatud konsoolis.
koormatud konsoolis.
Kasutab funktsioone
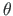 ja momendid
ja momendid 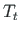 ,
,
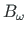 ,
,
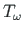 ning
ning 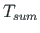 laus- ja koondkoormusega
laus- ja koondkoormusega 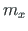 ,
, 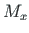 ning bimomendiga
ning bimomendiga
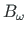 koormatud mitmesildelises talas.
koormatud mitmesildelises talas.
Kasutab funktsioone
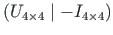 .
.
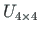 .
.
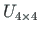 .
.
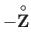 .
.
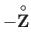 .
.
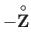 .
.
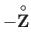 .
.
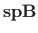 hõredasse maatriksisse
hõredasse maatriksisse
 , alustades
, alustades
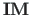 -nda rea ja
-nda rea ja
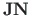 -nda veeru lõikekohast. Hõredate maatriksite
-nda veeru lõikekohast. Hõredate maatriksite
 ja
ja
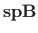 kattuvad elemendid liidetakse.
kattuvad elemendid liidetakse.
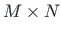 )-järku maatriksi
)-järku maatriksi
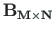 (
(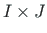 )-järku maatriksisse
)-järku maatriksisse
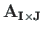 , alustades
, alustades
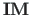 -nda rea ja
-nda rea ja
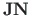 -nda veeru lõikekohast.
-nda veeru lõikekohast.
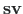 hõreda maatriksi
hõreda maatriksi

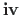 -nda rea
-nda rea
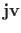 -nda veeru lõikekohale.
-nda veeru lõikekohale.andres