Järgmine: 2.3.1.3 Koondbimoment konsoolil Üles: 2.3.1 Ülekandevõrrandite lahenduste testimine Eelmine: 2.3.1.1 Lausmoment konsoolil
Andmed. Konsooli pikkus
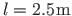 . Konsooli otsa b on ekstsentriliselt rakendatud jõud
. Konsooli otsa b on ekstsentriliselt rakendatud jõud
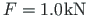 .
Vertikaalse koormuse
.
Vertikaalse koormuse 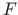 ekstsentrilisus
ekstsentrilisus
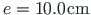 . Ristlõike kooldejäikus
. Ristlõike kooldejäikus
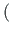 EIω
=
EIω
=
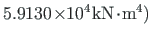 , vabaväändejäikus
, vabaväändejäikus
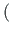 GIt =
GIt =
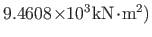 ja kooldekarakteristik
ja kooldekarakteristik
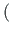 κ =
κ =
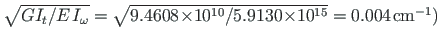 on konstantsed.
on konstantsed.
Lahendus. Vaatleme konsooli ühe elemendina, siis sisesidemed [Jür85, lk 8-9] puuduvad. Rajatingimuste 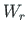 seadmisel on arvestatud energiateoreemi (B.8).
seadmisel on arvestatud energiateoreemi (B.8).
Siit saab jälgida, milline rajatingimus on antud ja milline leitakse.
Esimesel toel on toetingimuste paarides
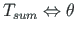 ja
ja
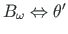 antud väändenurk θ = 0 ja suhteline väändenurk θ'
antud väändenurk θ = 0 ja suhteline väändenurk θ'
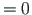 . Seega on esimene tugi jäik ning ei
võimalda pööret ega kooldumist.
Tundmatud on bimoment Bω
ja koguväändemoment Tsum.
. Seega on esimene tugi jäik ning ei
võimalda pööret ega kooldumist.
Tundmatud on bimoment Bω
ja koguväändemoment Tsum.
Konsooli lõpus on antud bimoment Bω
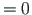 ja koguväändemoment Tsum
ja koguväändemoment Tsum
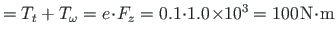 . Tundmatuks jäävad väändenurk θ ja suhteline väändenurk θ'
(
. Tundmatuks jäävad väändenurk θ ja suhteline väändenurk θ'
(
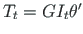 ).
).
Rajaväärtuste arvutamiseks kasutame nagu EST-meetodi [Lah97a], [Lah14] puhulgi hõredat võrrandisüsteemi 2.11
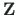 on võrrandisüsteemi tundmatute vektor
on võrrandisüsteemi tundmatute vektor
Muutuja
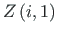 indeks (i=1, 2, 3,
indeks (i=1, 2, 3,  , 8) on toodud joonisel 2.7.
, 8) on toodud joonisel 2.7.
Põhivõrrandites (2.84) [Lah12, jn 14.9] 2.12
sisalduva laiendatud ülekandemaatriksi
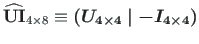 (2.87)
arvutamiseks saab kasutada GNU Octave'i funktsiooni yspWGvfmhvI.m.
(2.87)
arvutamiseks saab kasutada GNU Octave'i funktsiooni yspWGvfmhvI.m.
Võrrandisüsteemis (2.100) on tundmatuid poole rohkem kui võrrandeid. Kanname need võrrandid võrrandisüsteemi (2.97) (vt väljavõte programmist 2.4).
# Tala hõreda laiendatud ülekandemaatriksi arvutus
spvF=yspWGvfmhvI(baasi0,l,GIt,EIw);
%vB=yzWGmx(baasi0,l,l,a,mx,GIt,EIw); # koormusvektori arvutus
IIv=1;
IJv=1;
%vB=vB.*(-1);
# sisestab ülekandemaatriksi võrrandisüsteemi spA*Z=Bvb
spA=spInsertBtoA(spA,IIv,IJv,spvF);
% # sisestab koormusvektori võrrandisüsteemi vabaliikmesse Bv
%Bvb=InsertBtoA(Bvb,NNK,1,IIv,1,vB,4,1);
# võrrandisüsteemi vabaliige Bvb on eelnevalt nullitud
Võrrandisüsteemis (2.97) peab olema võrrandeid ja tundmatuid ühepalju. Võrrandite arv
peab ühtima maatriksi
 astakuga. Puuduvad sõltumatud võrrandid saame
kinemaatilistest ja staatilistest rajatingimustest (vt jaotis 3.1).
astakuga. Puuduvad sõltumatud võrrandid saame
kinemaatilistest ja staatilistest rajatingimustest (vt jaotis 3.1).
Järgnevalt
Rajatingimuste püstitus. Väliste rajatingimuste seadmisel tuleb arvestada energiateoreemi 2.13 (B.8).
Kui avaldistes
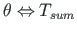 ,
,
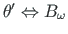 üks pool (pöördenurk
üks pool (pöördenurk 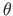 , suhteline väändenurk
, suhteline väändenurk
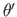 ) on antud, siis teine pool (koguväändemoment
) on antud, siis teine pool (koguväändemoment 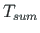 , bimoment
, bimoment
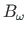 ) on tundmatu.
) on tundmatu.
Konsoolil on sõlmes a jäik tugi, mis ei võimalda pööret ega kooldumist (vt tabel 1.2). Tundmatud on bimoment Bω ja koguväändemoment Tsum . Viimases on vabaväändemoment Tt = 0 antud. Tundmatuks jääb kooldeväändemoment Tω .
Konsooli otsas, sõlmes b, on antud bimoment Bω
ja koguväändemoment Tsum
. Tundmatuks jäävad pöördenurk 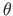 ja suhteline väändenurk
ja suhteline väändenurk
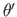 (
(
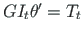 ).
).
Koostatud on neli rajatingimuse võrrandit. Sisestame need võrrandisüsteemi (2.97) (vt väljavõte programmist 2.5). Võrrandisüsteemi astak võrdub tundmatute arvuga. Järelikult on sisestatud võrrandid lineaarselt sõltumatud.
####### Rajatingimused
spA=spSisestaArv(spA,5,1,1); # $theta_A$ - väändenurk
spA=spSisestaArv(spA,6,2,1); # $T_tA$ - kooldeväändemoment
spA=spSisestaArv(spA,7,7,1); # $B_{L}$ - bimoment
spA=spSisestaArv(spA,8,6,1); # $T_{tL}+ T_{\omega L}$
spA=spSisestaArv(spA,8,8,1); # - üldväändemoment
Bvb(8,1)=10000.0 ;
#vastavad vabaliikmed Bvb on juba nullitud
spA_rank = sprank(spA) # võrrandisüsteemi astak
Sisestatud võrrandisüsteemi kordajad hõredas maatriksis spA on esitatud arvutuspäeviku väljavõttes 2.5.
spA = Compressed Column Sparse (rows = 8, cols = 8, nnz = 20 [31%])
(1, 1) -> 1 (5, 1) -> 1 (1, 2) -> -26.425 (2, 2) -> -1 (6, 2) -> 1 (1, 3) -> 0.057403 (2, 3) -> 0.0047008 (3, 3) -> -1.5431 (4, 3) -> -0.0047008 (1, 4) -> 4.6297 (2, 4) -> 0.54308 (3, 4) -> -293.80 (4, 4) -> -1.5431 (1, 5) -> -1 (2, 6) -> -1 (8, 6) -> 1 (3, 7) -> -1 (7, 7) -> 1 (4, 8) -> -1 (8, 8) -> 1
Algparameetrite arvutus.
Rajaväärtuste leidmisel korrutasime väändenurgad skaleerimisteguriga:
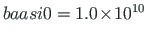 . Skaleerimata algparameetrite saamiseks tuleb vastavad suurused jagada skaleerimisteguriga. Konsooli skaleerimata algparameetrid
on toodud arvutuspäeviku väljavõttes 2.6.
. Skaleerimata algparameetrite saamiseks tuleb vastavad suurused jagada skaleerimisteguriga. Konsooli skaleerimata algparameetrid
on toodud arvutuspäeviku väljavõttes 2.6.
Algparameetrid - AP1
theta - 0.0000e+00
Tt - 0.0000e+00
B - 1.9040e+06
Tw - -1.0000e+04
Väändenurkade ja väändemomentide arvutus.
Väändenurkade ja väändemomentide leidmiseks konsooli ristlõigetes
kasutame ülekandevõrrandit (![]() )
)
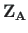 on konsooli algparameetrid (vt arvutuspäeviku väljavõte 2.6). Ülekandemaatriksi
on konsooli algparameetrid (vt arvutuspäeviku väljavõte 2.6). Ülekandemaatriksi
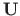 leiame GNU Octave'i funktsiooniga ylWGfhlin.m (vt väljavõte programmist 2.6).
leiame GNU Octave'i funktsiooniga ylWGfhlin.m (vt väljavõte programmist 2.6).
AP=AlgPar(:,1) baasi0=1.0 Nmitmeks=4 xx=0; xsamm=l/Nmitmeks; for ij=1:Nmitmeks+1 # 5 - displacements and forces at x=0.0 Xloikes(ij,1)=xx; vvF=ylWGfhlin(baasi0,l,xx,GIt,EIw); % vvB=yzWGmx(baasi0,l,xx,a,mx,GIt,EIw); # koormusvektori arvutus Fvv(1:4,ij)=vvF*AP % +vvB; Fvv(5,ij)=Fvv(2,ij)+Fvv(4,ij); xx=xx+xsamm; endfor
baasi0 = 1
Nmitmeks = 4
k = 0.0050000
x= 0.00 50.00 100.00 150.00 200.00
theta - 0.000e+00 -3.169e-04 -1.029e-03 -1.881e-03 -2.748e-03
Tt - 0.000e+00 -2.987e+03 -4.277e+03 -4.580e+03 -4.542e+03
B - 3.277e+06 1.611e+06 5.477e+05 2.185e+04 -9.313e-10
Tw - -4.000e+04 -2.701e+04 -1.572e+04 -5.420e+03 4.542e+03
Tsum - -4.000e+04 -3.000e+04 -2.000e+04 -1.000e+04 -2.001e-11
x = 177.1936900000
theta - -2.354e-03
Tt - -4.561e+03
B - -5.173e+04
Tw - 1.333e-03
Tsum - -4.561e+03
Leitud tulemuste põhjal koostame epüürid koondmomendist konsoolil (jn 2.8).
EST-meetodiga saadud tulemused on kooskõlas raamatus [Bõt62] jõu- ja deformatsioonimeetodi abil leitutega (vt tabel 2.3).
| x [cm] | Z(x) | [Sad63] | Mõõtühik | EST-meetod | Mõõtühik |
| 0.0 | θ | rad | 0.000×100 | rad | |
| Tt | 0.00 | kG·cm | 0.000×100 | N·cm | |
| Bω | –1.904×105 | kG·cm2 | –1.904×106 | N·cm2 | |
| Tω | 1.000×103 | kG·cm | 1.000×104 | N·cm | |
| Tsum | 1.000×103 | kG·cm | 1.000×104 | N·cm | |
| 62.5 | θ | rad | 5.632×10–7 | rad | |
| Tt | kG·cm | 1.610×103 | N·cm | ||
| Bω | kG·cm2 | –1.332×106 | N·cm2 | ||
| Tω | kG·cm | 8.390×103 | N·cm | ||
| Tsum | kG·cm | 1.000×104 | N·cm | ||
| 125 | θ | rad | 2.011×10–6 | rad | |
| Tt | 2.69×102 | kG·cm | 2.692×103 | N·cm | |
| Bω | –8.440×104 | kG·cm2 | –8.442×105 | N·cm2 | |
| Tω | 7.31×102 | kG·cm | 7.308×103 | N·cm | |
| Tsum | 1.000×103 | kG·cm | 1.000×104 | N·cm | |
| 187.5 | θ | rad | 4.020×10–6 | rad | |
| Tt | kG·cm | 3.316×103 | N·cm | ||
| Bω | kG·cm2 | –4.093×105 | N·cm2 | ||
| Tω | kG·cm | 6.684×103 | N·cm | ||
| Tsum | kG·cm | 1.000×104 | N·cm | ||
| 250 | θ | rad | 6.300×10–6 | rad | |
| Tt | 3.52×102 | kG·cm | 3.519×103 | N·cm | |
| Bω | 0.00 | kG·cm2 | 4.657×10–10 | N·cm2 | |
| Tω | 6.48×102 | kG·cm | 6.481×103 | N·cm | |
| Tsum | 1.00×103 | kG·cm | 1.000×104 | N·cm |
andres