Järgmine: B.2 Varrassüsteemi rajaülesanne Üles: B. Töö õhukeseseinalise varda Eelmine: B. Töö õhukeseseinalise varda
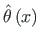 ja integreerime üle varda l:
ja integreerime üle varda l:
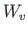 väändel
väändel
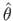 . Lisame koondkoormuse
. Lisame koondkoormuse
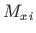 töö (
töö (
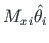 ) varda telje punkti i siirdel
) varda telje punkti i siirdel
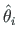 . Seega
. Seega
Alustame võrrandi (B.2) vasaku poole esimesest liikmest:
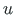 ja
ja
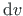 järgmiselt:
järgmiselt:
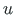 ja
ja
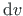 järgmiselt:
järgmiselt:
Arvestades avaldisi (B.4), (B.5), (B.6) ja (B.7), võime
võrrandi (B.2) esitada virtuaaltööde (passiivtööde)
summana:
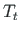 ja kooldeväändemoment
ja kooldeväändemoment
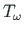 moodustavad koguväändemomendi
moodustavad koguväändemomendi
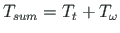 .
.
Võttes arvesse, et rajajõudude töö 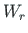 ja
koormuse töö
ja
koormuse töö 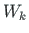 summa moodustab
välisjõudude töö
summa moodustab
välisjõudude töö
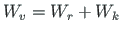 , saame elastsete varrassüsteemide
energiateoreemi [Din11, lk 112]
, saame elastsete varrassüsteemide
energiateoreemi [Din11, lk 112]
Rajajõudude töö avaldisele võib anda kuju
Sisejõudude töö saab avaldada ka nii:
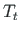 ja bimomendi
ja bimomendi
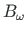 avaldisi
avaldisi
andres