Järgmine: 1.6.3 Seos üldväändemomendi ja Üles: 1.6 Sisejõududevahelised seosed Eelmine: 1.6.1 Seos kooldepingete vahel
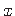 järgi:
järgi:
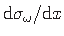 kooldenihkepinge
tuletisega
kooldenihkepinge
tuletisega
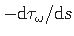 (vt avaldis (1.34)) ja pinnaelemendi
(vt avaldis (1.34)) ja pinnaelemendi
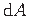 keskjoone pikkusele vastava elemendiga
keskjoone pikkusele vastava elemendiga
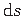 (
(
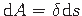 ):
):
Integreerime võrrandi (1.37) parempoolseimat liiget ositi valemi
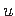 ja
ja 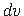 järgmiselt:
järgmiselt:
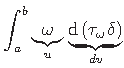 |
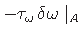 nulliga, sest varda välispinnal (sektorkoordinaadi
nulliga, sest varda välispinnal (sektorkoordinaadi
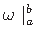 äärmistes punktides)
kooldenihkepinged puuduvad:
äärmistes punktides)
kooldenihkepinged puuduvad:
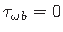 ,
,
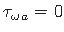 .
.
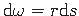 (vt jaotis
(vt jaotis 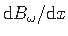 - bimomendi tuletis varda teljesuunalise koordinaadi
- bimomendi tuletis varda teljesuunalise koordinaadi 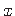 järgi - on võrdne kooldeväändemomendiga Tω.
järgi - on võrdne kooldeväändemomendiga Tω.
Seostest (1.19) ja (1.42) saame kooldeväändemomendi
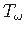 :
:
andres