1.5 Tasakaaluvõrrandid ristlõike kõverdumisel
Vaatleme pingete jaotust ristlõikes takistatud väändel:
- vabaväändele vastavad nihkepinged
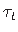 (jn 1.12 a) ristlõike
keskjoonel (jn A.1) puuduvad, seina paksuses muutuvad lineaarselt;
(jn 1.12 a) ristlõike
keskjoonel (jn A.1) puuduvad, seina paksuses muutuvad lineaarselt;
- kooldenormaalpinged σω
(jn 1.13) on seina paksuses konstantsed;
- kooldenihkepinged τω
(jn 1.12 b) on seina paksuses konstantsed.
Joonis 1.11.
Kooldenormaalpinged U-profiilis
|
|
![\includegraphics[width=65mm]{joonised/secNormaalpinged1.eps}](imgPtk1v105.png)
|
![\includegraphics[width=38mm]{joonised/secNormaalpinged2.eps}](imgPtk1vv108.png)
|
|
|
|
|
|
|
|
|
|
|
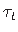 (jn 1.12 a) ristlõike
keskjoonel (jn A.1) puuduvad, seina paksuses muutuvad lineaarselt;
(jn 1.12 a) ristlõike
keskjoonel (jn A.1) puuduvad, seina paksuses muutuvad lineaarselt;