Järgmine: A.6 Sektorkoordinaadi peanullpunkt Üles: A. Õhukeseseinalise varda ristlõike Eelmine: A.4.2 Sektorkoordinaadi pooluse muutmine
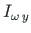 ,
,
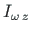 on
võrdsed nulliga, nimetatakse lõikekeskmeks [KMPR12, lk 233] (sks Schubmittelpunkt, ingl shear center, vn
on
võrdsed nulliga, nimetatakse lõikekeskmeks [KMPR12, lk 233] (sks Schubmittelpunkt, ingl shear center, vn 
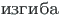 ).
).
Kasutatud on ka terminit paindekese [Jür85, lk 229]. Varda lõikekeskmeid ühendavat joont nimetame elastseks teljeks
(sks Schubmittelachse, ingl elastic axis e line of shear centers, vn 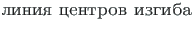 ).
).
Õhukeseseinalise varda pinnakeskmes võtame kasutusele parema käe teljestiku, kus y ja z on peateljed.
Sel juhul võrduvad nulliga nii ristlõikepinna staatilised momendid 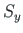 ja
ja 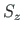 kui ka
tsentrifugaalmoment
kui ka
tsentrifugaalmoment
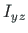 :
:
Tingimusi (A.43) ja (A.44) arvestades leiame võrranditest (A.45) ja (A.46) lõikekeskme koordinaadid 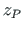 ja
ja 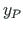 :
:
Valemeid (A.47) ja (A.48) kasutatakse ka siis, kui esialgne poolus 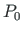 ei asu pinnakeskmes.
Nüüd tuleb nende abil leitud lõikekeskme koordinaatidele
ei asu pinnakeskmes.
Nüüd tuleb nende abil leitud lõikekeskme koordinaatidele 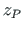 ,
, 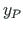 lisada pooluse P kaugus pinnakeskmest.
lisada pooluse P kaugus pinnakeskmest.
Kui ristlõikepinnal on sümmeetriatelg, siis asub pinna lõikekese sellel teljel.
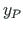 (
(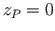 ).
Ristlõikepinna sektortsentrifugaalmomendid
).
Ristlõikepinna sektortsentrifugaalmomendid
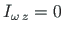 (A.27) ja
(A.27) ja
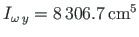 (A.28).
(A.28).
Leiame ristlõike inertsimomendi 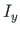 ja lõikekeskme koordinaadi
ja lõikekeskme koordinaadi 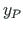 :
:
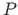 kaugus keskjoonest on
kaugus keskjoonest on
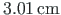 . Ristlõike keskme
. Ristlõike keskme 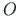 ja
lõikekeskme
ja
lõikekeskme 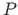 vaheline kaugus on
vaheline kaugus on
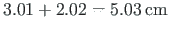 (
(
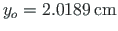 (A.26)).
(A.26)).
Punktide 1, 2, 3 ja 4 (jn A.13 b) sektorkoordinaadid:
andres