Järgmine: A.5 Lõikekese Üles: A.4 Sektorkoordinaadi teisendused Eelmine: A.4.1 Sektorkoordinaadi alguspunkti muutmine
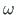 tema pooluse
tema pooluse 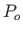 üleviimisel punkti P (jn A.12 a). Võtame kasutusele parema käe teljestiku, mille
puhul on raadiusvektori pööre vastupäeva positiivne.
üleviimisel punkti P (jn A.12 a). Võtame kasutusele parema käe teljestiku, mille
puhul on raadiusvektori pööre vastupäeva positiivne.
Sektorkoordinaadi diferentsiaalid
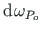 (poolus
(poolus 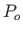 ) ja
) ja
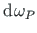 (poolus
(poolus 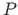 ):
):
Jooniselt A.12 a näeme, et
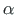 tähistab nurka keskjoone puutuja
tähistab nurka keskjoone puutuja
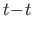 (punktis M) ja z-telje vahel.
Jooniselt A.12 b saame seosed
(punktis M) ja z-telje vahel.
Jooniselt A.12 b saame seosed
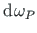 (A.33)
kirjutame kujul
(A.33)
kirjutame kujul
andres