Järgmine: A.4 Sektorkoordinaadi teisendused Üles: A. Õhukeseseinalise varda ristlõike Eelmine: A.2.3 Simpsoni 3/8-valem
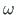 – sektorpindala e sektorkoordinaat;
– sektorpindala e sektorkoordinaat;
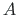 – ristlõike pindala.
– ristlõike pindala.
Kui ristlõikes on lõike ühtlase paksusega
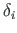 , siis staatilise sektormomendi arvutus lihtsustub.
Keskjoone elemendi ds pikkusele vastava pinnaelemendi dA pindala on siis
, siis staatilise sektormomendi arvutus lihtsustub.
Keskjoone elemendi ds pikkusele vastava pinnaelemendi dA pindala on siis
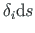 .
.
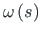 ,
,
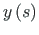 ja
ja
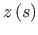 graafikud (epüürid).
graafikud (epüürid).
Pooluse
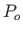 ja koordinaadi alguspunkti M valime keskjoonel nii, nagu on näidatud joonisel A.10 a . Pooluse
ja koordinaadi alguspunkti M valime keskjoonel nii, nagu on näidatud joonisel A.10 a . Pooluse 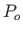 selline valik võimaldab arvutust lihtsustada. Punkti 1 sektorkoordinaat
selline valik võimaldab arvutust lihtsustada. Punkti 1 sektorkoordinaat
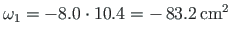 .
.
Ristlõike pinnakeskme asukoha leidmiseks arvutame esmalt ristlõike pindala A:
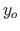 vertikaalsest keskjoonest
vertikaalsest keskjoonest