Järgmine: A.2.3 Simpsoni 3/8-valem Üles: A.2 Staatiline sektormoment Eelmine: A.2.1 Vereštšagini võte
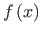 integreerimisel lõigu
integreerimisel lõigu
![$ \left[ a, b \right]$](imgLsA877.png) pikkusega l pooleks (l/2 ja l/2).
Siis
pikkusega l pooleks (l/2 ja l/2).
Siis 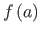 – funktsiooni väärtus lõigu alguses;
– funktsiooni väärtus lõigu alguses;
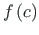 – funktsiooni väärtus lõigu keskel;
– funktsiooni väärtus lõigu keskel;
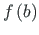 – funktsiooni väärtus lõigu lõpus.
– funktsiooni väärtus lõigu lõpus.
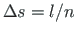 võtab
Simpsoni valem kuju
võtab
Simpsoni valem kuju
Joonisel A.9 a on funktsioonide
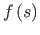 ja
ja
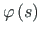 epüüride ordinaadid sama märgiga.
Joonisel A.9 b on funktsioonide ordinaatidel epüüride otstes erinevad märgid. Korrutise integraali arvutamiseks rakendame Simpsoni valemit (A.14)
epüüride ordinaadid sama märgiga.
Joonisel A.9 b on funktsioonide ordinaatidel epüüride otstes erinevad märgid. Korrutise integraali arvutamiseks rakendame Simpsoni valemit (A.14)
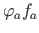 ,
,
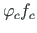 ja
ja
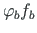 positiivsed, kui
epüüride ordinaadid on varda
samal poolel, ja negatiivsed, kui epüüride ordinaadid on vastandmärkidega. Näiteks joonisel A.9 b on lõigu algul (punktis
a) ja lõpus (punktis b) epüüride ordinaatide korrutis negatiivne,
kuna ordinaadid on suunatud eri poole. Lõigu keskel (punktis c)
on ordinaatide korrutis positiivne.
Simpsoni valem (A.16) annab täpse tulemuse lineaarsete
epüüride ning lineaarse ja ruutparaboolse epüüri korrutamisel.
Kõrgemat järku epüüride puhul tuleb kasutada Simpsoni 3/8-valemit
(A.22).
positiivsed, kui
epüüride ordinaadid on varda
samal poolel, ja negatiivsed, kui epüüride ordinaadid on vastandmärkidega. Näiteks joonisel A.9 b on lõigu algul (punktis
a) ja lõpus (punktis b) epüüride ordinaatide korrutis negatiivne,
kuna ordinaadid on suunatud eri poole. Lõigu keskel (punktis c)
on ordinaatide korrutis positiivne.
Simpsoni valem (A.16) annab täpse tulemuse lineaarsete
epüüride ning lineaarse ja ruutparaboolse epüüri korrutamisel.
Kõrgemat järku epüüride puhul tuleb kasutada Simpsoni 3/8-valemit
(A.22).
Numbrilisel integreerimisel Simpsoni valemiga (A.16) kasutame
arvutusprogrammi GNU Octave. Korrutame vektorid a (A.17) ja b (A.18) elementide kaupa (Hadamard'iA.4 korrutis) A.5.
Korrutamise tulemuseks on avaldis (A.19).
Võtame kasutusele Simpsoni valemi kordajaid sisaldava vektori
 ,
mille transponeeritud kuju on
,
mille transponeeritud kuju on
Elementi elemendiga korrutades saadud tulemuse (A.19) korrutame
skalaarselt
vektoriga (A.20). Tulemuseks on
Simpsoni valem (A.16)