Järgmine: A.2.1 Vereštšagini võte Üles: A. Õhukeseseinalise varda ristlõike Eelmine: A.1 Sektorkoordinaat
Õhukeseseinalise varda ristlõike pinnaelemendi staatiliseks sektormomendiks nimetatakse
pinnaelemendi dA ja sektorkoordinaadi 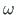 korrutist.
Kogu kujundi staatiline sektormoment
korrutist.
Kogu kujundi staatiline sektormoment
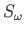 määratakse integraalina pindala A ulatuses:
määratakse integraalina pindala A ulatuses:
Kui ristlõikes leidub sirgeid lõike ühtlase paksusega
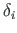 , siis staatilise sektormomendi arvutus lihtsustub.
Sel juhul avaldub keskjoone elemendi ds pikkusele vastav pinnaelement dA (jn A.5 a)
kujul
, siis staatilise sektormomendi arvutus lihtsustub.
Sel juhul avaldub keskjoone elemendi ds pikkusele vastav pinnaelement dA (jn A.5 a)
kujul
Nüüd saame avaldada staatilise sektormomendi (A.3):
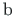 )
pindala diferentsiaali
)
pindala diferentsiaali
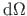 seosega
seosega
Esmalt leiame staatilise sektormomendi punktides 1, 2, 3 ja 4: