Järgmine: A.2 Staatiline sektormoment Üles: A. Õhukeseseinalise varda ristlõike Eelmine: A. Õhukeseseinalise varda ristlõike
A.1 Sektorkoordinaat
Õhukeseseinalise varda ristlõikest väljaspool võtame kasutusele punkti P
(jn A.2), mida nimetame pooluseks. Keskjoonel valime koordinaadi alguspunktiks M.
Raadiusvektor 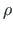 määrab punkti M asukoha keskjoonel.
määrab punkti M asukoha keskjoonel.
Meelevaldse punkti N asukoha keskjoonel saame avaldada määratud integraaliga:
- kus
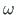 – sektorpindala e sektorkoordinaat;
– sektorpindala e sektorkoordinaat;
- r – pooluse P kaugus keskjoone puutujast, mis läbib punkti N;
-
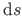 – keskjoone diferentsiaal.
– keskjoone diferentsiaal.
Integraalis olev suurus
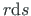 on võrdne kolmnurga
on võrdne kolmnurga 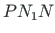 kahekordse pindalaga.Keskjoonega eraldatud sektorisse
kahekordse pindalaga.Keskjoonega eraldatud sektorisse 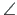 MPN jääva kujundi kahekordne pindala on võrdne sektorkoordinaadiga
MPN jääva kujundi kahekordne pindala on võrdne sektorkoordinaadiga
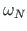 (A.1).
(A.1).
Võtame kasutusele parema käe teljestiku (jn A.3), mille puhul
raadiusvektori 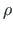 pööre vastupäeva on positiivne.
pööre vastupäeva on positiivne.
Joonisel on näidatud positiivse pöördenurga suund. Vaadates telje positiivsest otsast, loeme pöörde positiivseks z-teljest x-telje suunas, x-teljest y-telje suunas ja y-teljest z-telje suunas.
Sektorkoordinaadi muutuse õhukeseseinalise varda ristlõikes saab esitada graafikuna. Nimetame seda graafikut sektorkoordinaatide epüüriks. Kõverjoonelise keskjoone puhul on sektorkoordinaat mittelineaarne funktsioon muutujast s ja tema graafik on kõverjooneline. Keskjoone sirgjoonelisele osale vastav sektorkoordinaat on lineaarne funktsioon muutujast s.
Valime pooluseks punkti P ja sektorkoordinaadi alguspunktiks M (
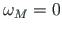 ). Arvutame punktide 1, 2, 3 ja 4 sektorkoordinaadid (raadiusvektori
). Arvutame punktide 1, 2, 3 ja 4 sektorkoordinaadid (raadiusvektori 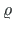 pööre vastupäeva on positiivne).
pööre vastupäeva on positiivne).
Leitud sektorkoordinaatide väärtuste (A.2) põhjal koostame ristlõike sektorkoordinaatide epüüri (jn A.4 b).
andres
2016-04-13
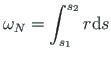
![\includegraphics[width=70mm]{joonised/seckoord.eps}](imgLsA829.png)
![\includegraphics[width=65mm]{joonised/vptelg.eps}](imgLsA834.png)
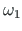
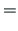
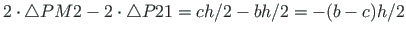
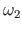
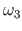
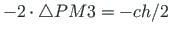
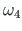
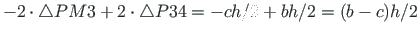
![\includegraphics[width=115mm]{joonised/seckoordEpyyr1.eps}](imgLsA844.png)