Järgmine: A.2.2 Simpsoni valem Üles: A.2 Staatiline sektormoment Eelmine: A.2 Staatiline sektormoment
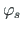 saab avaldada seosest
saab avaldada seosest
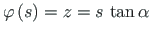 .
Integraali teisendame kujule
.
Integraali teisendame kujule
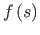 staatiline moment telje
staatiline moment telje 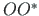 suhtes
suhtes
Integraalis (A.11) asendame
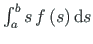 avaldisega (A.12).
Jooniselt
A.7 näeme, et
avaldisega (A.12).
Jooniselt
A.7 näeme, et
 =
= 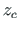 , kus
, kus 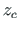 on lineaarselt muutuvas epüüris
on lineaarselt muutuvas epüüris
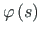 epüüri
epüüri
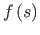 pindala
pindala 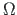 raskuskeskme kohal olev ordinaat.
Eelnenut arvesse võttes avaldame integraali (A.11)
järgmiselt:
raskuskeskme kohal olev ordinaat.
Eelnenut arvesse võttes avaldame integraali (A.11)
järgmiselt:
Seega on epüüride
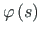 ,
,
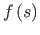 ordinaatide korrutise
integraal lõigul
ordinaatide korrutise
integraal lõigul
![$ \left[ a, b \right]$](imgLsA877.png) võrdne korrutisega, mille üheks
teguriks on epüüri pindala
võrdne korrutisega, mille üheks
teguriks on epüüri pindala 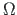 ja teiseks teguriks lineaarselt muutuvas epüüris ordinaat
ja teiseks teguriks lineaarselt muutuvas epüüris ordinaat 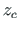 ,
mis on kohakuti pindala
,
mis on kohakuti pindala 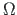 raskuskeskmega (jn A.7).
Korrutis
raskuskeskmega (jn A.7).
Korrutis
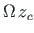 on positiivne, kui koormusest põhjustatud
epüür
on positiivne, kui koormusest põhjustatud
epüür
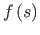 ja ordinaat
ja ordinaat 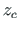 on sama märgiga.
Joonisel A.8 on näidatud lihtsate epüüride pindalad ja nende
raskuskeskmete kaugused.
Epüüri raskuskeskme arvutamise asemel on lihtsam kasutada Simpsoni
valemit.
on sama märgiga.
Joonisel A.8 on näidatud lihtsate epüüride pindalad ja nende
raskuskeskmete kaugused.
Epüüri raskuskeskme arvutamise asemel on lihtsam kasutada Simpsoni
valemit.