Järgmine: 1.5 Tasakaaluvõrrandid ristlõike kõverdumisel Üles: 1. Põhimõisted Eelmine: 1.3 Siirete ja deformatsioonide
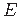 seoses (1.14) nimetatakse (normaal)elastsusmooduliks (ka Youngi1.12 mooduliks). Asendades deformatsiooni
seoses (1.14) nimetatakse (normaal)elastsusmooduliks (ka Youngi1.12 mooduliks). Asendades deformatsiooni 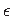 avaldises (1.14) tema avaldisega (1.13),
saame
avaldises (1.14) tema avaldisega (1.13),
saame
kus
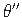 – väändenurga θ teine tuletis koordinaadi
– väändenurga θ teine tuletis koordinaadi 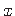 järgi.
järgi.
Praktilisteks arvutusteks moodustame kooldenormaalpinge
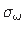 ja
bimomendi Bω
(jn 1.4) vahelise seose analoogiliselt tugevusõpetuses kasutatava normaalpinge
ja
bimomendi Bω
(jn 1.4) vahelise seose analoogiliselt tugevusõpetuses kasutatava normaalpinge 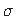 ja paindemomendi
ja paindemomendi 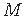 vahelise seosega [KMPR12].
Korrutame avaldist (1.15) sektorkoordinaadiga
vahelise seosega [KMPR12].
Korrutame avaldist (1.15) sektorkoordinaadiga 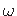 ja ristlõike
elementaarpindalaga
ja ristlõike
elementaarpindalaga
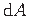 ning integreerime pindala A ulatuses.
ning integreerime pindala A ulatuses.
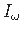 (A.60):
(A.60):
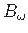 ja sektorinertsimomendi
ja sektorinertsimomendi
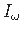 avaldised (1.17), (1.18),
saame seose (1.16) esitada kujul
avaldised (1.17), (1.18),
saame seose (1.16) esitada kujul 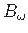 õhukeseseinalise varda ristlõikes on momendipaar (jn 1.4), mis staatilises mõttes on tasakaalustatud. Bimomendi leidmist vaatleme edaspidi. Avaldame suuruse
õhukeseseinalise varda ristlõikes on momendipaar (jn 1.4), mis staatilises mõttes on tasakaalustatud. Bimomendi leidmist vaatleme edaspidi. Avaldame suuruse
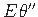 seosest (1.19):
seosest (1.19): 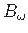 ja sektorinertsimoment Iω
ristlõikes ei muutu. Muutub ainult sektorkoordinaat
ja sektorinertsimoment Iω
ristlõikes ei muutu. Muutub ainult sektorkoordinaat 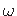 .
Seega sarnaneb kooldenormaalpingete
.
Seega sarnaneb kooldenormaalpingete
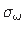 epüür sektorkoordinaadi
epüür sektorkoordinaadi 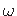 epüüriga.
epüüriga.
Raamatus [HIM11, lk 3] toodud märkuses rõhutatakse, et bimomendi ja kooldemomendi mõistet
ei tohi segi ajada. Bimomendi suuruseks on jõud korrutatud pikkuse ruuduga, kooldemomendi
suuruseks aga jõu ja pikkuse korrutis.
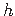 – ristlõike kõrgus;
– ristlõike kõrgus;
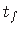 – vöö paksus1.13.
– vöö paksus1.13.  ) määrame vastavalt bimomendi märgireeglile (jn 1.18). Vaadates piki momendipaari õlga, tuleb avaldises (1.22) vaatajapoolse momendi määramisel võtta miinusmärk, vaatajast kaugema momendi määramisel aga plussmärk.
Vaatajapoolne moment on positiivne pöördumisel vastupäeva. Vaatajast kaugem moment on positiivne pöördumisel päripäeva. Siin on kasutatud parema käe teljestiku (jn A.3) märgireegleid.
) määrame vastavalt bimomendi märgireeglile (jn 1.18). Vaadates piki momendipaari õlga, tuleb avaldises (1.22) vaatajapoolse momendi määramisel võtta miinusmärk, vaatajast kaugema momendi määramisel aga plussmärk.
Vaatajapoolne moment on positiivne pöördumisel vastupäeva. Vaatajast kaugem moment on positiivne pöördumisel päripäeva. Siin on kasutatud parema käe teljestiku (jn A.3) märgireegleid.