Järgmine: A.9 Valemid sektorinertsimomendi määramiseks Üles: A. Õhukeseseinalise varda ristlõike Eelmine: A.7 Peasektorkoordinaadid
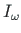 on integraalina väljenduv summa:
on integraalina väljenduv summa:
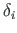 , siis sektorinertsimomendi arvutus lihtsustub:
, siis sektorinertsimomendi arvutus lihtsustub:
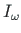 .
Peasektorkoordinaatide epüür on joonisel A.14 b .
Numbrilisel integreerimisel kasutame Simpsoni valemit (A.16). Eelnevalt leiame peasektorkoordinaatide epüüril
keskmised väärtused
.
Peasektorkoordinaatide epüür on joonisel A.14 b .
Numbrilisel integreerimisel kasutame Simpsoni valemit (A.16). Eelnevalt leiame peasektorkoordinaatide epüüril
keskmised väärtused
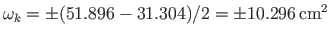 .
.
andres