Järgmine: B. Töö õhukeseseinalise varda Üles: A. Õhukeseseinalise varda ristlõike Eelmine: A.8 Sektorinertsimoment
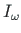 , lõikekeskme kauguse e
keskjoonest
ja ristlõike väändeinertsimomendi
, lõikekeskme kauguse e
keskjoonest
ja ristlõike väändeinertsimomendi 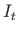 arvutamiseks kasutame valemeid tabelist
,,Properties of Sections"
A.6 A.7.
arvutamiseks kasutame valemeid tabelist
,,Properties of Sections"
A.6 A.7.
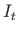 ning ristlõike sektorinertsimomendi
ning ristlõike sektorinertsimomendi
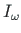 :
:
Arvutamisel rakendame GNU Octave'i programmi ohukeU(b,h,tf,tw).
Programmis kasutatavad parameetrid b, h, tf ja tw on
U-profiili (jn A.15) mõõtmed. Need võtame jooniselt A.13 a:
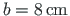 ,
,
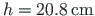 , vöö paksus
, vöö paksus
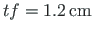 , seina paksus
, seina paksus
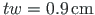 .
.
Arvutustulemused on toodud arvutuspäeviku väljavõttes A.1.
Võrdleme saadud tulemusi näites A.4 leitud lõikekeskme ja keskjoone vahekaugusega
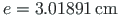 (A.50) ning näites A.7 leitud sektorinertsimomendiga
(A.50) ning näites A.7 leitud sektorinertsimomendiga
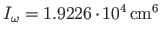 . Võrdlus näitab, et programmiga arvutatud tulemused
ühtivad näidetes leitutega.
. Võrdlus näitab, et programmiga arvutatud tulemused
ühtivad näidetes leitutega.
octave:1> secU=ohukeU(8,20.8,1.2,0.9)
=========================================
e | It | Iw
-----------------------------------------
secU =
3.0189e+00 1.4270e+01 1.9226e+04
-----------------------------------------
octave:2>
andres