Järgmine: 1.10 Koormused Üles: 1. Põhimõisted Eelmine: 1.8 Kooldenihkepinged ja pikikoormus
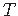 ja väändenurga
ja väändenurga
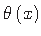 pööre vastupäeva ümber varda teljega paralleelse x-telje positiivne
(vt märgireegel [Bõt62, lk 166], mis erineb raamatus [KMPR12, lk 30] kasutatust).
pööre vastupäeva ümber varda teljega paralleelse x-telje positiivne
(vt märgireegel [Bõt62, lk 166], mis erineb raamatus [KMPR12, lk 30] kasutatust).
Varda otste välispinnal mõjuvaid rajajõude vaatleme kui välisjõude, täpsemini, kui reaktsiooni mõjuvale koormusele. Reaktsioonijõud määratakse tasakaalutingimustest. Rajajõudude märgi määramisel on kasutusel kaks märgikokkulepet. Esimene märgikokkulepe (jn 1.17 a) on tuttav tugevusõpetusest [MR96, lk 10, jn 8]. Teine märgikokkulepe (jn 1.17 b) on vajalik varrassüsteemide tasakaaluvõrrandite algoritmide koostamiseks.
Märgikokkuleppeid võrreldes näeme, et rajajõudude suunad varda lõpus ühtivad, varda alguses on aga vastandmärgilised.
Bimoment Bω õhukeseseinalise varda ristlõikes on staatilises tasakaalus momendipaar (jn 1.18). Bimomendi tekitavad kooldumist takistavad kooldenormaalpinged σω (jn 1.4).
Kui vaadata piki momendipaari õlga (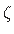 -telje suunas), siis loeme bimomendi
-telje suunas), siis loeme bimomendi
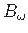 (jn 1.18) positiivseks juhul, kui vaatajapoolne moment pöörab vastupäeva ning vaatajast kaugem moment pöörab päripäeva (jn 1.18 b).
Reegel kehtib olenemata sellest, millises suunas
(jn 1.18) positiivseks juhul, kui vaatajapoolne moment pöörab vastupäeva ning vaatajast kaugem moment pöörab päripäeva (jn 1.18 b).
Reegel kehtib olenemata sellest, millises suunas 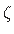 -telge vaadata.
-telge vaadata.
Kontrollime bimomendi märgireegli kehtivust valemiga (1.21) näite 1.1 abil.
U-profiili ristlõikes on antud positiivne bimoment
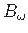 . U-profiili ristlõike punktides 1, 2, 3 ja 4 on
leitud kooldenormaalpinged, mille epüür on toodud joonisel 1.11. Joonisel 1.11 a
näidatud kooldenormaalpinged tekitavad bimomendi
. U-profiili ristlõike punktides 1, 2, 3 ja 4 on
leitud kooldenormaalpinged, mille epüür on toodud joonisel 1.11. Joonisel 1.11 a
näidatud kooldenormaalpinged tekitavad bimomendi
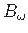 , mis vastab eespool olevale bimomendi märgireeglile.
Siin on peasektorkoordinaatide leidmisel kasutatud parema käe teljestikku, mille puhul on
raadiusvektori
, mis vastab eespool olevale bimomendi märgireeglile.
Siin on peasektorkoordinaatide leidmisel kasutatud parema käe teljestikku, mille puhul on
raadiusvektori  pööre vastupäeva positiivne.
pööre vastupäeva positiivne.
andres