Järgmine: 1.9 Märgikokkulepped väändel Üles: 1. Põhimõisted Eelmine: 1.7 Kooldenihkepinged
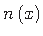 (jn 1.16). Näitame, et pikikoormuse
(jn 1.16). Näitame, et pikikoormuse
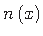 olemasolul ei kehti avaldis (1.42), s.t
olemasolul ei kehti avaldis (1.42), s.t
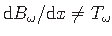 [Bõt62].
[Bõt62].
Vaatleme õhukeseseinalise varda elementi ABCD mõõtmetega
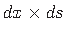 (jn 1.16),
kus
(jn 1.16),
kus
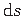 on keskjoone diferentsiaal (jn A.2).
on keskjoone diferentsiaal (jn A.2).
Vaadeldaval elemendil läbib pikikoormus
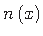 ristlõike punkti
ristlõike punkti
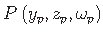 .
Siin on
.
Siin on
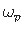 punkti
punkti 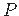 sektorkoordinaat (jn A.2). Ristlõike paksuse suunas
ebaühtlaselt jaotatud nihkepingete (vabaväände, St. Venant'i nihkepingete) mõju tähistame jaotatud väändemomendina
sektorkoordinaat (jn A.2). Ristlõike paksuse suunas
ebaühtlaselt jaotatud nihkepingete (vabaväände, St. Venant'i nihkepingete) mõju tähistame jaotatud väändemomendina 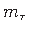 .
.
Ristlõikes mõjuvad veel kooldenormaalpinged σω
ja
kooldenihkepinged τω
.
Koostame vaadeldava elemendi tasakaaluvõrrandi x-teljele:
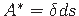 on lõikega eraldatud osa pindala.
on lõikega eraldatud osa pindala.
Ristlõikes (koordinaat 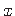 on fikseeritud) on elemendi paksus
on fikseeritud) on elemendi paksus 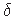 koordinaadi
koordinaadi 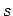 funktsioon, mis
lubab
funktsioon, mis
lubab 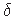 tuua osatuletise märgi alt välja. Jagades avaldise ka
tuua osatuletise märgi alt välja. Jagades avaldise ka 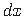 -iga, saame
-iga, saame
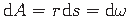 (vt (A.1)).
(vt (A.1)).
Asendame kooldenihkepinged valemis (1.63) nende avaldisega (1.62):
Kui sektorkoordinaat 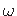 algab peanullpunktist, siis võrdub kogu ristlõike staatiline sektormoment nulliga:
algab peanullpunktist, siis võrdub kogu ristlõike staatiline sektormoment nulliga:
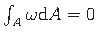 (vt avaldist (1.29)).
(vt avaldist (1.29)).
Kooldeväändemomendi
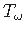 saab nüüd esitada kujul
saab nüüd esitada kujul
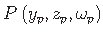 , mida läbib pikikoormuse
, mida läbib pikikoormuse
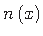 mõjusirge (jn 1.16).
mõjusirge (jn 1.16).
Diferentseerime bimomenti Bω
(1.19) x-koordinaadi järgi:
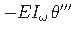 avaldises (1.66) bimomendi
tuletisega (1.67):
avaldises (1.66) bimomendi
tuletisega (1.67):
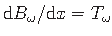 (1.42)
ei kehti koormamisel pikikoormusega
(1.42)
ei kehti koormamisel pikikoormusega
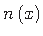 .
.
andres