Järgmine: 1.8 Kooldenihkepinged ja pikikoormus Üles: 1. Põhimõisted Eelmine: 1.6.3 Seos üldväändemomendi ja
Koostame tasakaaluvõrrandi x-teljele:
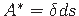 on lõikega
on lõikega
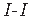 eraldatud osa pindala.
eraldatud osa pindala.
Asendame kooldenormaalpinge
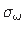 avaldises (1.47)
tema avaldisega (1.15) ja jagame
avaldises (1.47)
tema avaldisega (1.15) ja jagame
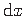 -iga:
-iga:
Tähistame joonisel 1.15 lõikega
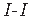 eraldatud osa staatilise sektormomendi (A.3) tähisega Sω
:
eraldatud osa staatilise sektormomendi (A.3) tähisega Sω
:
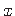 järgi ning jagame sektorinertsimomendiga Iω
:
järgi ning jagame sektorinertsimomendiga Iω
:
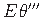 avaldisse (1.51).
Valemis (1.52) saame bimomendi
avaldisse (1.51).
Valemis (1.52) saame bimomendi
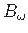 tuletise varda teljesuunalise koordinaadi
tuletise varda teljesuunalise koordinaadi 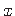 järgi asendada
kooldeväändemomendiga
Tω
(1.42).
järgi asendada
kooldeväändemomendiga
Tω
(1.42).
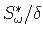 on maksimaalne.
on maksimaalne.
Avaldis (1.53) on struktuurilt sarnane tugevusõpetuses kasutatava Zuravski valemiga [KMPR12].
 .
.
Selle ristlõike sektorinertsimoment Iω
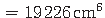 (A.62).
Suurim kooldenihkepinge on ülemises vöös, kus eraldatud osa staatiline sektormoment
(A.62).
Suurim kooldenihkepinge on ülemises vöös, kus eraldatud osa staatiline sektormoment
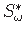 on
minimaalne. Staatilise sektormomendi
on
minimaalne. Staatilise sektormomendi
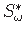 arvutamisel kasutame valemit (A.7).
Selleks leiame peasektorkoordinaatide nulli asukoha joonisel 1.10 b kujutatud sarnastest kolmnurkadest.
arvutamisel kasutame valemit (A.7).
Selleks leiame peasektorkoordinaatide nulli asukoha joonisel 1.10 b kujutatud sarnastest kolmnurkadest.
andres