Järgmine: 1.4 Kooldenormaalpinged Üles: 1. Põhimõisted Eelmine: 1.2 Vaba ja takistatud
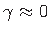 ;
;
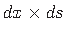 (jn 1.5).
(jn 1.5).
Nihkedeformatsiooni varda keskpinnal käsitleme kui kõrgemat järku väikest suurust:
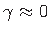 .
.
Ristkülikulise elemendi punkti 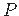 (jn 1.6) siirete komponendid koordinaadi
(jn 1.6) siirete komponendid koordinaadi 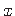 ja sektorkoordinaadi
ja sektorkoordinaadi 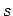 (vt jaotis A.1) suunas
tähistame vastavalt
(vt jaotis A.1) suunas
tähistame vastavalt
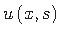 ja
ja
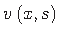 . Ristkülikulise elemendi punkti
. Ristkülikulise elemendi punkti 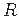 siirete komponendid
siirete komponendid
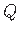 siirete komponendid
siirete komponendid
Ristkülikulise elemendi deformeerumisel (jn 1.6) moodustub nihkenurk 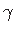 nurkade
nurkade 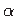 ja
ja 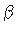 summana:
summana:
Tingimuse (1.5) rakendamine õhukeseseinalise varda keskpinnal moodustab esimese hüpoteesi sisu.
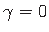 ) võib elemendi siirdumist ja pöördumist vaadelda kui jäiga keha pööret. Ristkülikulise elemendi PRQD (jn 1.5 ja 1.7) kontuur ei deformeeru.
) võib elemendi siirdumist ja pöördumist vaadelda kui jäiga keha pööret. Ristkülikulise elemendi PRQD (jn 1.5 ja 1.7) kontuur ei deformeeru.
Kahe ristlõike pööret teineteise suhtes ümber varda telje x mõõdame väändenurgaga 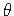 .
Vlassovi teooria [Vla59] teise hüpoteesi põhjal on väändenurk θ
ainult
varda teljesuunalise koordinaadi x funktsioon.
.
Vlassovi teooria [Vla59] teise hüpoteesi põhjal on väändenurk θ
ainult
varda teljesuunalise koordinaadi x funktsioon.
Ristlõike pöördumisel ümber telje, mis on paralleelne varda teljega (joonisel 1.8 on näidatud ristlõike keskjoone pööre ümber pooluseks nimetatava punkti P), võime keskjoone
puutujasuunalise elementaarsiirde
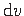 kirjutada kujul
kirjutada kujul
kus
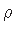 – raadiusvektor poolusest
– raadiusvektor poolusest 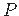 vaadeldavasse punkti
vaadeldavasse punkti 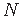 (jn 1.8 ja jaotis A.1);
(jn 1.8 ja jaotis A.1);
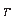 – pooluse
– pooluse 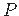 kaugus keskjoone puutujast
kaugus keskjoone puutujast
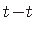 , mis läbib vaadeldavat punkti
, mis läbib vaadeldavat punkti 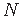 ;
;
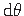 – elementaarväändenurk.
– elementaarväändenurk.
Nihkenurga
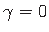 puudumise tingimusest (1.5) saame
puudumise tingimusest (1.5) saame
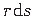 asendada sektorkoordinaadi diferentsiaaliga
asendada sektorkoordinaadi diferentsiaaliga
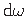 (A.33):
(A.33):
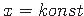 , saab siirde
, saab siirde
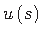 leida avaldisega
leida avaldisega
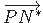 projektsiooni pikkus (jn 1.8) ristlõiketasandil
pärast ristlõike kooldumist võrdne raadiusvektori
projektsiooni pikkus (jn 1.8) ristlõiketasandil
pärast ristlõike kooldumist võrdne raadiusvektori
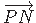 esialgse pikkusega.
Õhukeseseinalise varda ristlõike kontuur ei deformeeru (jn 1.9a), seega jääb kaugus kahe ristlõikes asuva punkti vahel deformeerimise käigus muutumatuks (jn 1.9b).
esialgse pikkusega.
Õhukeseseinalise varda ristlõike kontuur ei deformeeru (jn 1.9a), seega jääb kaugus kahe ristlõikes asuva punkti vahel deformeerimise käigus muutumatuks (jn 1.9b).