2.3 Põhivõrrandid takistatud väändel

Avaldame õhukeseseinalise varda takistatud väände põhivõrrandid maatrikskujul

$$\mathbf{Z_{L}\left( x\right) } = \mathbf{U}\cdot\mathbf{Z_{A}} + \mathbf{\stackrel{\rm\circ}{Z}}$$ (2.83)

kus

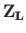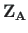$\mathbf{Z_{L}}$, $\mathbf{Z_{A}}$ - avaldisega (2.75) näidatud väändenurgad ja väändemomendid varda lõpus ning alguses;

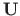$\mathbf{U}$ - ülekandemaatriks (2.76).

Õhukeseseinalise varda takistatud väände põhivõrrandid teise märgikokkuleppe puhul (2.83) saab kirjutada võrrandisüsteemina

$$\mathbf{U}\cdot\mathbf{Z_{A}} -\mathbf{I_{4\times4}\cdot Z_{L}} = \mathbf{ - \stackrel{\rm\circ}{Z}}$$ (2.84)

Lühemalt

$$\mathbf{\widehat{UI}}_{4\times8}\cdot\mathbf{\widehat{Z}} = \mathbf{-\stackrel{\rm\circ}{Z}}$$ (2.85)

kus

$$\mathbf{\widehat{Z}} = \left[\begin{array}{c} \mathbf{Z_{A}} \\ \mathbf{Z_{L}} \end{array}\right]$$ (2.86)

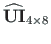$\mathbf{\widehat{UI}}_{4\times8}$ - laiendatud ülekandemaatriks ${\left( U_{4\times 4}\mid -I_{4\times 4}\right)}$:

$$\mathbf{\widehat{UI}}_{4\times8} = \left[ \begin{array}{cccc} 1 &... ...-\mathrm{ch}\hspace*{1pt}{{{\kappa x}}\hspace*{1pt}} \end{array}\right] - \quad$$

$$\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \vspace*{3pt} \\ 0 & 1 ... ...& 1 & 0 \vspace*{3pt} \\ 0 & 0 & 0 & 1 \end{array}\right] \hspace*{15pt} \quad$$ (2.87)

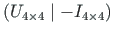ning koormusvektor 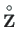$\mathrm{\mathbf{\stackrel{\rm\circ}{Z}}}$ lausmomendiga 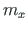$m_{x}$ avaldub

$$%%\resizebox{0.69\hsize}{!}{$ \mathbf{\stackrel{\rm\circ}{Z}} = \... ...a\right)_{+}}\hspace*{1pt}} \right]} \end{array}\right] <tex2html_comment_mark>$$ (2.88)

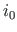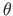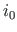Siin on $i_{0}$ väändenurga $\theta$ skaleerimistegur (võrrandisüsteemiga (2.85) leitavad väändenurgad on $i_{0}$ korda suuremad).

Iga varda ülekandevõrrandite (2.85) kohta lisame neli rajatingimust.