2.2 Ülekandemaatriks takistatud väändel
Õhukeseseinalise varda takistatud väände ülekandemaatriksi koostamiseks teise märgikokkuleppe järgi vaatleme väändenurga tuletiste ja momentide vahelisi seoseid:
Väändenurga ja väändemomentide seosed saame algparameetritest,
võttes väändenurgast tuletised (2.33)-(2.36) ja korrutades need vastava jäikusega (2.67)-(2.69).
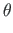 |
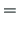 |
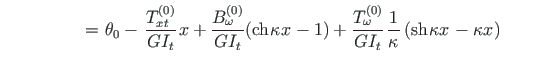 |
(2.70) |
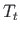 |
 |
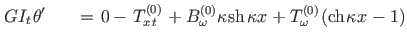 |
(2.71) |
 |
 |
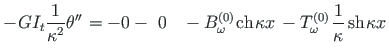 |
(2.72) |
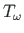 |
 |
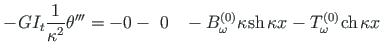 |
(2.73) |
Esitame võrrandid (2.70)-(2.73) maatrikskujul
 |
|
|
(2.74) |
kus
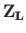 ,
,
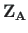 on varda lõpus ja alguses olevad väändenurgad ning väändemomendid
on varda lõpus ja alguses olevad väändenurgad ning väändemomendid
![$\displaystyle \mathbf{Z_{L}} =
\left[\begin{array}{c}
{\theta}_{L} \\
{T_{t}}_...
...left( 0\right)}_{\omega} \\
{T ^{\left( 0\right)}_{\omega}}
\end{array}\right]$](imgPtk2v439.png) |
|
|
(2.75) |
ja ülekandemaatriks
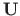 teise märgikokkuleppe puhul
teise märgikokkuleppe puhul
![$\displaystyle \mathbf{U} =
\left[ \begin{array}{cccc}
1 & - { \frac{1}{GI_{t}}}...
...& -\mathrm{ch}\hspace*{1pt}{{{\kappa x}}\hspace*{1pt}}
\end{array}\right] \quad$](imgPtk2v441.png) |
|
|
(2.76) |
Alajaotised
andres
2016-04-11
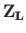 ,
,
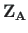 on varda lõpus ja alguses olevad väändenurgad ning väändemomendid
on varda lõpus ja alguses olevad väändenurgad ning väändemomendid
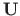 teise märgikokkuleppe puhul
teise märgikokkuleppe puhul