Järgmine: 2.2 Ülekandemaatriks takistatud väändel Üles: 2.1 Takistatud väände diferentsiaalvõrrandid Eelmine: 2.1.4 Homogeenne diferentsiaalvõrrand
 lauskoormusega
lauskoormusega
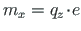 (jn 1.19 a) ekvivalentne koguväändemoment (2.1)), kus
(jn 1.19 a) ekvivalentne koguväändemoment (2.1)), kus
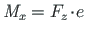 ning e on jõu
ning e on jõu 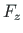 kaugus lõikekeskmeid ühendavast teljest (jn 1.19 b);
kaugus lõikekeskmeid ühendavast teljest (jn 1.19 b); 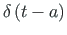 - Dirac'i 2.4 deltafunktsioon.
- Dirac'i 2.4 deltafunktsioon.
Mittehomogeense diferentsiaalvõrrandi (2.37) erilahendit
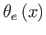 (2.22) otsime Cauchy2.5
valemi [Sad63, lk 40], [Ste59] abil:
(2.22) otsime Cauchy2.5
valemi [Sad63, lk 40], [Ste59] abil:
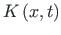 on vastava homogeense diferentsiaalvõrrandi normeeritud lahend.
on vastava homogeense diferentsiaalvõrrandi normeeritud lahend.
Täpsemalt,
Siin kasutame normeeritud lahendite fundamentaalsüsteemi (2.28):
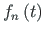 :
:
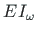 :
:
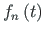 esitada kujul
esitada kujul
Vaatleme juhtu, kui
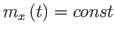 . Erilahendi (2.39) saamiseks tuleb integreerida avaldis
. Erilahendi (2.39) saamiseks tuleb integreerida avaldis
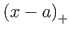 on Heaviside'i2.6 funktsioon
on Heaviside'i2.6 funktsioon
Mittehomogeense diferentsiaalvõrrandi (2.37) teisele vabaliikmele
(
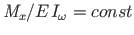 ) vastava erilahendi saame avaldist (2.39)
integreerides:
) vastava erilahendi saame avaldist (2.39)
integreerides:
Lisame bimomendi
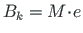 erilahendi:
erilahendi:
Lisame erilahendid
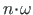 jaoks:
jaoks:
Tabelis 1.1 esitatud koormuste jaoks on koostatud diferentsiaalvõrrandite erilahendite tabel 2.1.
Leiame erilahendi
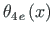 tuletised:
tuletised:
andres