Järgmine: 2.1.4 Homogeenne diferentsiaalvõrrand Üles: 2.1 Takistatud väände diferentsiaalvõrrandid Eelmine: 2.1.2 Väändenurga elastse joone
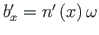 (võrdle avaldisega
(võrdle avaldisega
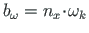 (1.79)).
(1.79)).
Diferentsiaalvõrrandi (2.21) lahendit otsime kujul
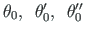 ja
ja
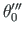 - otsitava funktsiooni väärtused kohal
- otsitava funktsiooni väärtused kohal
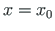 ;
; 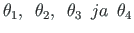 - homogeense
diferentsiaalvõrrandi normeeritud lahendite fundamentaalsüsteem 2.1 [Sad63, lk 39];
- homogeense
diferentsiaalvõrrandi normeeritud lahendite fundamentaalsüsteem 2.1 [Sad63, lk 39]; 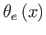 - mittehomogeense diferentsiaalvõrrandi erilahend.
- mittehomogeense diferentsiaalvõrrandi erilahend.
andres