2.1.2 Väändenurga elastse joone diferentsiaalvõrrand pikikoormusel
Koostame elemendile ABCD (jn 1.16) mõjuvate jõudude momentide võrrandi
elastse telje O-O suhtes:
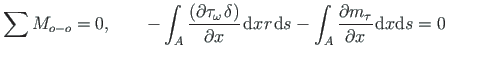 |
|
|
(2.12) |
kus r on pooluse 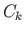 kaugus keskjoone puutujast (vt ka jn A.2).
kaugus keskjoone puutujast (vt ka jn A.2).
Taandame võrrandi (2.12)
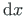 -iga ja asendame
-iga ja asendame
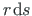 sektorkoordinaadi
diferentsiaaliga
sektorkoordinaadi
diferentsiaaliga
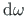 (vt jaotis
(vt jaotis ![[*]](./icons/crossref.png) ):
):
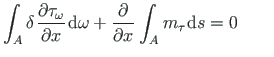 |
|
|
(2.13) |
Saadud võrrandi teise liikme teisendamisel
arvestame seost (1.57) ja vabaväändemomendi Tt avaldist (1.1):
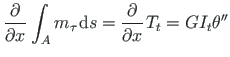 |
|
|
(2.14) |
Kooldenihkepingete avaldise (1.62) ja avaldise (2.14) kasutamine võimaldab võrrandi (2.13) esitada järgmisel
kujul:
![$\displaystyle \int_{A}\left[E{\hspace*{1pt}}\theta^{IV}\int_{A^{\ast}}\omega\hs...
...left(x\right)\right]{\mathrm{d}\omega} + GI_{t}\theta^{\prime\prime} = 0 \qquad$](imgPtk2v322.png) |
|
|
(2.15) |
Kirjutame viimase võrrandi kujule
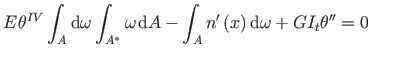 |
|
|
(2.16) |
Võrrandi (2.16) esimest liiget ositi integreerides (vt avaldis (1.65)) saame
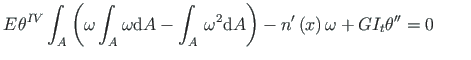 |
|
|
(2.17) |
Kui sektorkoordinaadi 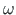 algus on sektorkoordinaadi peanullpunktis, siis võrdub kogu ristlõike staatiline sektormoment nulliga:
algus on sektorkoordinaadi peanullpunktis, siis võrdub kogu ristlõike staatiline sektormoment nulliga:
 (1.29).
Nüüd võtab võrrand (2.17) kuju
(1.29).
Nüüd võtab võrrand (2.17) kuju
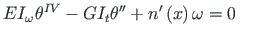 |
|
|
(2.18) |
Jagame saadud võrrandi kooldejäikusega
EIω:
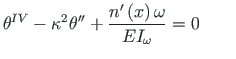 |
|
|
(2.19) |
kus κ on kooldekarakteristik
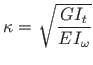 |
|
|
(2.20) |
Siin on
EIω kooldejäikus ja GIt vabaväändejäikus.
andres
2016-04-11
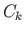 kaugus keskjoone puutujast (vt ka jn A.2).
kaugus keskjoone puutujast (vt ka jn A.2).
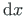 -iga ja asendame
-iga ja asendame
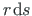 sektorkoordinaadi
diferentsiaaliga
sektorkoordinaadi
diferentsiaaliga
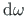 (vt jaotis
(vt jaotis ![]() ):
):
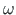 algus on sektorkoordinaadi peanullpunktis, siis võrdub kogu ristlõike staatiline sektormoment nulliga:
algus on sektorkoordinaadi peanullpunktis, siis võrdub kogu ristlõike staatiline sektormoment nulliga:
 (1.29).
Nüüd võtab võrrand (2.17) kuju
(1.29).
Nüüd võtab võrrand (2.17) kuju